


Next: 3. Reference Manual
Up: 2. User's Guide
Previous: 15. The Iota Constructor
Subsections
16. Syntax: Parsing and Printing
The purpose of this chapter is threefold:
- 1.
- To explain the relation between syntax and IMPS expressions.
- 2.
- To explain the default syntax, which we refer to as the ``string
syntax,'' and briefly to explain how you can extend or modify this syntax.
- 3.
- To explain how you can redefine the syntax altogether.16.1
As explained in Chapter 7, expressions are variables,
constants, and compound expressions formed by applying constructors to
other expressions. Expressions can thus be represented as Lisp
s-expressions:
- Formal symbols (i.e., constants or variables) correspond to atoms.
- Compound expressions correspond to certain lists of the form
where
each ci is itself an expression.
In the implementation, an expression is a data structure which also caches
a large amount of information such as the free and bound variables of
the expression, the constants contained in the expression, the home
language of the expression, and so on.
For the IMPS user, an expression is typically something which can be
represented as text, for instance
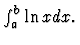 The
correspondence of an expression as a data structure to an external
representation for input or output is determined by the user syntax
which is employed. IMPS allows multiple user syntaxes, so for
example, the syntax that is used for reading in expressions (usually
text) may be different from the syntax used to display expressions
(which could be text or text interspersed with TEX commands which
would make the output suitable for input to the TEX processor.) This
flexible arrangement means users can freely change from one syntax to
another, even during the course of an interactive proof.
The
correspondence of an expression as a data structure to an external
representation for input or output is determined by the user syntax
which is employed. IMPS allows multiple user syntaxes, so for
example, the syntax that is used for reading in expressions (usually
text) may be different from the syntax used to display expressions
(which could be text or text interspersed with TEX commands which
would make the output suitable for input to the TEX processor.) This
flexible arrangement means users can freely change from one syntax to
another, even during the course of an interactive proof.
The process of building an IMPS expression from user input can be broken up
into two steps:
- 1.
- Parsing a string into an s-expression s.
- 2.
- Building an IMPS expression from the s-expression s.
Similarly, the process of
displaying an expression also consists of two parts:
- 1.
- Building an s-expression s from an IMPS expression.
- 2.
- Providing some representation of s as a string.
The phases ``string to s-expression'' for reading and ``s-expression
to string'' for printing are under direct user control. They can be
modified by resetting the following switches:
To write your own reader and printer procedures, you will have to do
some programming in the T language. However, some reader and printer procedures are
particularly easy to write. For example to write your own reader and
printer for s-expression syntax, you could evaluate the following s-expressions:
(set (imps-reader)
(lambda (l port) (read port)))
(set (imps-printer)
(lambda (s-exp port) (pretty-print s-exp port)))
In the next section we describe the default syntax
which is similar to the syntax of some computer algebra systems.
We begin with some notation: if ``Term'' is a class of strings,
| Term* |
= |
zero or more comma-separated members of Term |
| Term+ |
= |
one or more comma-separated members of Term. |
A string is accepted by the string syntax exactly when
IMPS can build an s-expression s from it. Otherwise, IMPS will give you a parsing error. However, to say the string is accepted does not
mean that the system can build an IMPS expression from s. A number of
things could go wrong:
- An atom in s has no sort specification, so that IMPS assumes it is the name of a constant, but no such constant exists in
the language.
- The arguments of a function are of the wrong type, or there are
too many or too few arguments.
- A constructor was given components of the wrong type, or
the number of components is wrong.
The tables 16.1, 16.2, and 16.3 are
a description of those sequences of characters accepted by the string
syntax. This description is fairly close to a BNF grammar, but fails
to be one since some of the expression categories (such as the
category of binary infix operators or the category of
quasi-constructors) are only specified partially or not at all. This
is because these expression categories depend on parts of the state of
the IMPS system, which are likely to change from user to user.
We also want to stress that these tables say nothing about how strings
are parsed into nested lists (and much less about what the strings
mean mathematically.) For example, one cannot say how argument
associations are disambiguated from these tables alone. The table of
operator precedences in the next section specifies this information.
The syntax tables are thus of limited value and should only be
consulted to get a very rough idea of what expressions look like.
Table 16.1:
Description of String Syntax 1
| Exp |
::= |
Aexp |
|
| |
|
Oxp(Oxp*) |
Function application |
| |
|
Exp BInfxOp Exp |
Binary infix application |
| |
|
(Oxp) |
Parenthesized Oxp |
| |
|
Exp oo Exp |
Composition |
| |
|
Oxp =Oxp |
|
| |
|
Oxp ==Oxp |
|
| |
|
not Exp |
|
| |
|
Exp and Exp |
|
| |
|
Exp or Exp |
|
| |
|
Exp implies Exp |
|
| |
|
Exp iff Exp |
|
| |
|
Binder(Binding* , Exp) |
Binders (including with) |
| |
|
iota(Atom:Sort, Exp) |
|
| |
|
if(Exp, Exp, Exp+) |
Requires an odd number of Exp |
| |
|
Qc{Exp+} |
Prefix quasi-constructor Exp |
| |
|
Qc{Exp+,Sort} |
Prefix quasi-constructor Exp |
| |
|
?Sort |
Undefined from sort |
| |
|
#(Exp,Sort) |
Sort definedness assertion |
| |
|
#(Exp) |
Definedness assertion |
| Oxp |
::= |
Exp |
Operator or expression |
| |
|
PrefxOp |
|
| |
|
LogfxOp |
|
| |
|
BInfxOp |
|
| |
|
PostfxOp |
|
| Aexp |
::= |
Num |
Numerical constants |
| |
|
Atom |
Variables & other constants |
|
Table 16.2:
Description of String Syntax 2
| Sort |
::= |
Asort |
These are base sorts |
| |
|
[Sort,Sort+] |
N-ary function sort constructor. |
| Binder |
::= |
lambda |
|
| |
|
forall |
|
| |
|
forsome |
|
| |
|
with |
|
| Binding |
::= |
Sortdecl+ |
|
| Sortdecl |
::= |
Atom+ : Sort |
|
PrefxOp |
::= |
comb |
Combinatorial coefficients |
| |
|
lim |
Limit operator for sequences |
| LogfxOp |
::= |
- |
|
| BInfxOp |
::= |
* |
|
| |
|
+ |
|
| |
|
< |
|
| |
|
<= |
|
| |
|
i-in |
|
| |
|
i-subset |
|
| PostfxOp |
::= |
! |
|
|
Table 16.3:
Description of Atoms
| Atom |
::= |
TextChar followed by TextChar's or Digit's |
| |
|
SpecialSeq |
| |
|
SpecialSeq followed by _ and TextChar's or Digit's |
| TextChar |
::= |
a
 z |
z | _ |% | $ | & |
| Digit |
::= |
0
 9
9 |
| SpecialSeq |
::= |
^ | * | + | - | ^^
| ** | ++ | ! | < | <= | > | >= |
|
The process of building an s-expression from an input
string, itself breaks up into two parts:
- Tokenization of the input string. This can be thought of as
dividing the input string into a list of substrings called
tokens.
- Parsing of the list of tokens. This can be thought of as
transforming a linear structure of tokens into a tree structure of
tokens.
The table below gives some examples of how a string s is translated into an s-expression
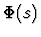 according to the string syntax.
according to the string syntax.
| String |
Reads |
 |
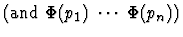 |
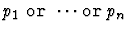 |
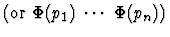 |
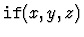 |
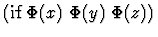 |
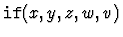 |
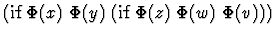 |
|
<tex2htmlverbmark>56<tex2htmlverbmark>(t,s) |
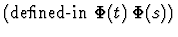 |
|
<tex2htmlverbmark>57<tex2htmlverbmark>(t) |
 |
| x + y |
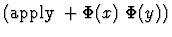 |
| x - y |
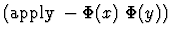 |
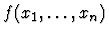 |
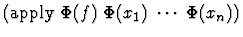 |
To build an s-expression from the input tokens, it is necessary to
disambiguate the tokens which are operators16.2 from the tokens which are arguments. The
association of tokens to operators is determined by the operator
binding powers. For example, the string x+2*3 is parsed as
because the
operator * has a higher binding power than +.
Table 16.4 is a list of the bindings of some common
operators.
Table 16.4:
Operator Binding Powers
| Operator |
Binding |
| + |
100 |
| - |
110 |
| * |
120 |
| / |
121 |
^ |
140 |
| ! |
160 |
| = |
80 |
| == |
80 |
| i-subset |
101 |
| i-in |
101 |
| > |
80 |
| >= |
80 |
| < |
80 |
| <= |
80 |
| not |
70 |
| iff |
65 |
| implies |
59 |
| and |
60 |
| or |
50 |
|
The string syntax can be modified or extended using the def-forms
def-parse-syntax and def-print-syntax. The use of
def-forms is documented in Chapter 17.
- 1.
- A parsing error is indicated by an error message
**Error: Parsing error:
This means IMPS was unable to
build an s-expression from your input. IMPS will provide some
indication as to where the error occurred.
Following are some examples of common parsing errors:
> (qr "with(a,b:rr a=b)")
** Error: Parsing error: Illegal token A encountered.
with(a,b:rr a <<== =b).
This error occurred because the variable sort specifications have to be followed
by a comma.
> (qr "forall(a,b:rr,a=b")
** Error: Parsing error: Expecting ":" or "," or ")".
forall(a,b:rr,a=b <<== .
This error results from a missing right parenthesis.
- 2.
- An error message of one of the following kinds
is usually an indication that the current theory
(this is the value of the switch (current-theory)) is
different from what you expected. This typically happens
when you begin an interactive proof of a formula without having set
the current theory to its desired value.
> (qr "with(x:rr,x=1)")
** Error: QUANTIFIER-DECODE-VAR-SUB-LIST:
RR is not a sort in
#{IMPS-basic-language 12: THE-KERNEL-LANGUAGE}.
This error message indicates that IMPS was unable to build an expression
in the current theory because there is no sort named rr.
> (qr "with(x:ind, x+x)")
** Error: SEXP->EXPRESSION-1:
Cannot locate + in
#{IMPS-basic-language 12: THE-KERNEL-LANGUAGE}.
This error message indicates that IMPS was unable to build an
expression in the current theory because there is no constant named
+. To remedy an error of the above type, reset the (current-theory) switch by using the menu.



Next: 3. Reference Manual
Up: 2. User's Guide
Previous: 15. The Iota Constructor
System Administrator
2000-07-23