


Next: 19. The Primitive Inference
Up: 3. Reference Manual
Previous: 17. The IMPS Special
Subsections
This chapter is intended to provide users with documentation for
IMPS proof commands. However, it is not suggested that users read
this chapter before using IMPS.
Commands can be used in two modes:
- Interactive mode. In this mode an individual command is invoked
by supplying the command's name. The system will then prompt you for
additional arguments.
- Script mode. In this mode a command is invoked by a
command form. Command forms are s-expressions
To use commands in this way, you must know the possible command
arguments. Commands in script mode can be invoked line by line, by
region, or in batch mode. Moreover, if the command requires no arguments, then
the name of the command by itself is a command form.
We will use the following template to describe use of
individual commands. (The last three entries are optional.)
- Script usage
- Describes the use of the command in scripts.
Arguments such as theories, macetes, and theorems are specified by
name. Some arguments can be specified in various ways. When an argument
is an assumption, it can be specified as follows:
- A nonnegative integer i. This denotes the i-th assumption.
- A string
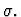 If
If 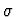 denotes an expression which is alpha-equivalent
to an assumption, then it denotes that assumption. If
denotes an expression which is alpha-equivalent
to an assumption, then it denotes that assumption. If 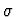 matches one
or more assumptions, then it refers to the first of those assumptions. Matching here
is done in a way that does not preserve scopes of binding constructors and places
only type constraints on the matching of variables.
matches one
or more assumptions, then it refers to the first of those assumptions. Matching here
is done in a way that does not preserve scopes of binding constructors and places
only type constraints on the matching of variables.
- Interactive argument retrieval.
- This tells you how arguments are requested in
the minibuffer when used interactively, with a brief description of each argument. In cases
where IMPS can determine that there is only one possible choice for an
argument, for example, if the argument is an index number for an assumption
when there is exactly one assumption, then IMPS will make this
choice and not return for additional input.
- Command Kind.
- Null-inference, single-inference, or multi-inference.
A null-inference command never adds any inference nodes to the
deduction graph. A single-inference commands adds exactly one
inference node to the deduction graph, when it is successful. A
multi-inference command adds more than one inference node to
the deduction graph in some cases.
- Description.
- A brief description of the command. Some
commands can be described as rules of inference in a logical calculus.
For each such command we use a table composed of the following units:
| Conclusion |
TEMPLATE |
| Premise |
TEMPLATE |
where the item TEMPLATE for the conclusion refers to the form for the
given goal (sequent), while the TEMPLATE item for the premise indicates the
form for the resulting subgoal. In general, there will be more than
one premise; moreover, in some cases we distinguish one particular
premise as a major premise. In so doing, we regard the remaining
premises as minor premises.
- Related commands.
- These are other commands you might
consider applying because, for example, they are quicker or more
effective for your task at hand.
- Remarks.
- Hints or observations that we think you should
find useful.
- Key binding.
- A single key to invoke the command.
To apply a command in interactive mode to the current sequent node
(that is, the one visible in the sequent node buffer), hit !. You can also apply a command by selecting it from the command menu
as follows:
- For Emacs version 19, click on the entry
Extend-DG in the menubar and select the option Commands.
- For Emacs version 18, click right on the Command menu item in
the Extending the Deduction Graph pane. You can also invoke
the command menu directly by pressing the key F3.
You will be presented with a well-pruned menu of those commands which
are applicable to the given sequent node. Once you select a command,
the system will request the additional arguments it needs to apply the
command. You will notice that for a given command, the system will
sometimes request additional arguments and at other times not do so.
In the cases where the system fails to make a request for arguments,
the system determines what these additional arguments should be on
its own.
For the precise definition of what a script is, see the section on the proof
script language in Chapter 12. Essentially a proof script is a
sequence of forms of the following kinds:
Each command form (that is, a form which begins with a command name)
instructs IMPS to do the following two things:
- Apply the command with name command-name to
the current sequent node with the arguments
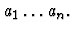
- Reset the current sequent node to be the first ungrounded relative.
To apply a single command in script mode to the current sequent node,
place the cursor on the first line of the command form and type C-c l. In order for the interface software to recognize the
form to execute, there cannot be more than one command form per line.
However, a single command form can occupy more than one line.
To apply in sequence the command forms within a region, type C-c
r.
antecedent-inference
(antecedent-inference assumption).
assumption can be given as an integer i or a string 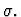
- 0-based index of antecedent formula -
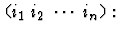 i.
i.
The
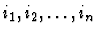 are the indices of the assumptions of sequent
node on which antecedent inferences can be done, that is an
implication, conjunction, disjunction, biconditional,
conditional-formula, or an existential formula. In case there is only
one such formula, this argument request is omitted.
are the indices of the assumptions of sequent
node on which antecedent inferences can be done, that is an
implication, conjunction, disjunction, biconditional,
conditional-formula, or an existential formula. In case there is only
one such formula, this argument request is omitted.
Single-inference.
| Conclusion |
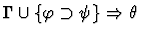 |
| Premises |
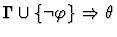 |
| |
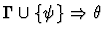 |
| Conclusion |
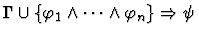 |
| Premise |
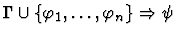 |
| Conclusion |
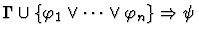 |
Premises
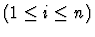 |
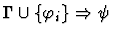 |
| Conclusion |
 |
| Premises |
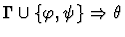 |
| |
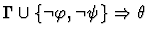 |
| Conclusion |
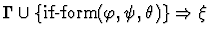 |
| Premises |
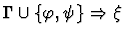 |
| |
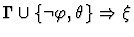 |
| Conclusion |
 |
| Premise |
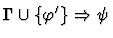 |
Notes:
- Each sequent in the preceding table is of
the form
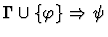 .
.
- The index of the assumption
 in context
in context
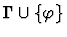 is i.
is i.
-
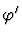 is obtained from
is obtained from  by renaming the
variables among
by renaming the
variables among
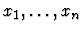 which are free in both
which are free in both  and
the original sequent.
and
the original sequent.
:
antecedent-inference-strategy
direct-and-antecedent-inference-strategy
direct-inference
Keep in mind that any antecedent inference produces subgoals which
together are equivalent to the original goal. Thus, it is always safe
to do antecedent inferences, in the sense that they do not produce
false subgoals from true ones.
a
antecedent-inference-strategy
(antecedent-inference-strategy
assumption-list).
assumption-list can be given as
a list of numbers, a list of strings, or an assumption-list form.
- List of formula indices for antecedent inferences -
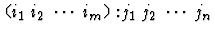 .
The
.
The
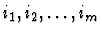 are the indices of the
assumptions of sequent node on which antecedent inferences can be
done, that is an implication, conjunction, disjunction, biconditional,
conditional-formula, or an existential formula. In case there is only
one such formula, this argument request is omitted.
are the indices of the
assumptions of sequent node on which antecedent inferences can be
done, that is an implication, conjunction, disjunction, biconditional,
conditional-formula, or an existential formula. In case there is only
one such formula, this argument request is omitted.
Multi-inference.
Call an assumption of the goal
sequent node fixed if its index is not among
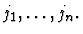 This command repeatedly applies the
antecedent-inference command to the goal node and resulting subgoal
nodes until the only possible antecedent inferences are on fixed
assumptions.
This command repeatedly applies the
antecedent-inference command to the goal node and resulting subgoal
nodes until the only possible antecedent inferences are on fixed
assumptions.
:
antecedent-inference
direct-and-antecedent-inference-strategy
This command is called as a subroutine by
a number of other commands including instantiate-theorem and
instantiate-universal-antecedent.
A
apply-macete
(apply-macete macete).
- Macete name: The name of a macete. Formally, a macete is a function which takes as arguments a context and an
expression and returns an expression. Macetes are used to apply a
theorem or a collection of theorems to a sequent in a deduction graph.
In order to use them effectively, read the section on macetes in the
manual.
Single-inference.
This command applies the argument
macete to the given sequent node.
:
apply-macete-locally
apply-macete-locally-with-minor-premises
apply-macete-with-minor-premises
Macetes are an easy and very effective
way of applying lemmas in a proof. In fact, in the course of
developing a theory, we suggest that some effort be expended in
formulating lemmas with a view to applying them as macetes.
m
apply-macete-locally
(apply-macete-locally macete expression occurrences).
- Macete name: The name of a macete.
- Expression to apply macete: A subexpression of the sequent
assertion to which you want to apply the macete.
- Occurrences of expression (0-based): The list occurrences of
the expression you want to apply the macete to.
Single-inference.
This command applies the argument
macete to the given sequent node at those occurrences of the
expression supplied in response to the minibuffer prompt.
:
apply-macete
apply-macete-locally-with-minor-premises
apply-macete-with-minor-premises
This command is useful when you need to
control where a macete is applied, in cases where it applies at
several locations. For example, if the sequent assertion is
| x+y2 | =
| y2+x |, then applying the macete
commutative-law-for-addition to the 0-th occurrence of
x+y2 yields a new sequent with assertion
|y2+x | = |
y2+x |. If the macete had been applied globally, the resulting
assertion would have been
|y2+x | = | x+y2|.
apply-macete-locally-with-minor-premises
(apply-macete-locally-with-minor-premises macete expression occurrences).
- Macete name: The name of a macete.
- Expression to apply macete: A subexpression of the sequent
assertion to which you want to apply the macete.
- Occurrences of expression (0-based): The list occurrences of
the expression you want to apply the macete to.
Single-inference.
This command applies the argument
macete to the given sequent node, in the same way as apply-macete-locally, but
with the following important difference: whenever the truth or
falsehood of a definedness or sort-definedness assertion cannot be
settled by the simplifier, the assertion is posted as a
additional subgoal to be proved.
:
apply-macete
apply-macete-locally
apply-macete-with-minor-premises
apply-macete-with-minor-premises
(apply-macete-with-minor-premises macete).
- Macete name: The name of a macete.
Single-inference.
This command applies the argument
macete to the given sequent node, in the same way as apply-macete, but
with the following important difference: whenever the truth or
falsehood of a convergence requirement cannot be settled by the
simplifier, the assertion is posted as a additional subgoal to be
proved.
:
apply-macete
apply-macete-locally
apply-macete-locally-with-minor-premises
The convergence requirements which are
posted as additional subgoals arise from two different sources:
- 1.
- Convergence requirements are generated by the simplifier
in the course of certain reductions, including algebraic
simplification and beta-reduction.
- 2.
- Convergence requirements are also generated by
checks that instantiations of universally valid formulas used by the
macete are sound.
You should never assume that subgoals generated by this command are
always true. As always for nonreversible commands, you should inspect
the new subgoals to insure IMPS is not misdirecting your proof.
assume-theorem
(assume-theorem theorem).
- Theorem name: The name of a theorem in the deduction
graph theory.
Single-inference.
This command adds the argument
theorem to the context of the given sequent.
:
apply-macete
assume-transported-theorem
instantiate-theorem
To apply a theorem to a sequent, you
will usually want to use apply-macete or instantiate-theorem instead of assume-theorem.
assume-transported-theorem
(assume-transported-theorem
theorem interpretation).
- Theorem name: The name of a theorem in T.
- Theory interpretation: The name of a theory
interpretation of T in the deduction graph's theory.
Single-inference.
This command transports the argument
theorem to the deduction graph's theory via the argument theory
interpretation. Then the transported theorem is added to the context
of the given sequent using assume-theorem.
:
apply-macete
assume-theorem
instantiate-transported-theorem
To apply a theorem to a sequent from
outside the deduction graph's theory, you will usually want to use
apply-macete or instantiate-transported-theorem
instead of assume-transported-theorem.
auto-instantiate-existential
auto-instantiate-existential.
None.
Multi-inference.
This command tries to instantiate an
existential assertion with terms from the context of the given
sequent.
:
auto-instantiate-universal-antecedent
instantiate-existential
auto-instantiate-universal-antecedent
(auto-instantiate-universal-antecedent
assumption). assumption can be given as an integer i or a string 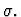
- 0-based index of universal antecedent formula -
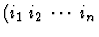 ): i. The
): i. The
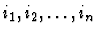 are
the indices of the universal assumptions of the sequent node. In case
there is only one universal antecedent formula, this argument request
is omitted.
are
the indices of the universal assumptions of the sequent node. In case
there is only one universal antecedent formula, this argument request
is omitted.
Multi-inference.
This command tries to instantiate the
i-th assumption of the context of the given sequent with terms from
the context.
:
auto-instantiate-existential
instantiate-universal-antecedent
backchain
(backchain
assumption). assumption can be given as an integer
i or a string 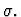
- 0-based index of antecedent formula: If
there is only one assumption, this argument request is omitted.
Single-inference.
This command includes the behavior described under backchain-through-formula. However, for a part of the assumption of
one of the forms s=t,  ,
,
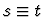 ,
if a subexpression
of the assertion matches s, then it is replaced by the corresponding
instance of t.
,
if a subexpression
of the assertion matches s, then it is replaced by the corresponding
instance of t.
:
backchain-backwards
backchain-repeatedly
backchain-through-formula
b
backchain-backwards
(backchain-backwards
assumption). assumption can be given as an integer
i or a string 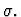
- 0-based index of antecedent formula:
Single-inference.
Backchain-backwards differs from backchain in that subformulas
of the assumption of the forms s=t,  ,
,
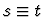 are
used from right to left.
are
used from right to left.
:
backchain
backchain-repeatedly
backchain-through-formula
backchain-repeatedly
(backchain-repeatedly
assumption-list). assumption-list can be given as a
list of numbers, of strings or an assumption-list form.
- List of 0-based indices of antecedent formulas:
If there is only one assumption, this
argument request is omitted.
Multi-inference.
A succession of backchains are performed using
the indicated assumptions. Execution terminates when every backchaining
opportunity against those assumptions has been used up.
:
backchain
backchain-backwards
backchain-through-formula
backchain-through-formula
(backchain-through-formula
assumption). assumption can be given as an integer i or a string 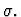
- 0-based index of antecedent formula: If
there is only one assumption, this argument request is omitted.
Single-inference.
This command attempts to use the assumption with the given index to
replace the assertion to be proved. In the simplest case, if the
given assumption is
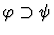 and the assertion is
and the assertion is  ,
then backchain-through-formula replaces the assertion with
,
then backchain-through-formula replaces the assertion with  .
Similarly, if the assertion is
.
Similarly, if the assertion is
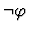 ,
it is replaced with
,
it is replaced with
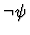 .
The command extends this simplest case in four ways:
.
The command extends this simplest case in four ways:
- If the assumption is universally quantified, then matching is used to
select a relevant instance.
- If the assumption is a disjunction
then, for any 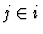 ,
it may be treated as
,
it may be treated as
- If the assumption is a conjunction, each conjunct is tried separately,
in turn.
- These rules are used iteratively to descend through the structure of
the assumption as deeply as necessary.
If IMPS cannot recognize that the terms returned by a match are defined
in the appropriate sorts, then these assertions are returned as additional
minor premises that must later be grounded to complete the derivation.
:
backchain
backchain-backwards
backchain-repeatedly
beta-reduce
beta-reduce.
None.
Single-inference.
This command
attempts to beta-reduce each lambda-application in the assertion of
the given sequent.
:
beta-reduce-antecedent
beta-reduce-insistently
beta-reduce-repeatedly
beta-reduce-with-minor-premises
simplify
Since beta-reduction can often be applied
several times in a row, the command beta-reduce-repeatedly is
usually preferable to this command. Beta-reduction is also performed
by simplify.
beta-reduce-antecedent
(beta-reduce-antecedent
assumption). assumption can be given as an integer
i or a string 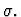
- 0-based index of antecedent-formula: i. If there is only
one assumption, this argument request is omitted.
Multi-inference.
This command is used for beta-reducing
an assumption in the context of the given sequent. It is equivalent
to the following sequence of commands: incorporate-antecedent
applied to the given sequent with argument i; beta-reduce-repeatedly applied to the sequent yielded by the previous
command; and direct-inference applied to the sequent yielded by
the previous command. The commands halts if beta-reduce-repeatedly grounds the first produced sequent.
:
beta-reduce-repeatedly
simplify-antecedent
The implementation of this command has
the side effect that the assertion is beta-reduced as well as the
antecedent formula.
beta-reduce-insistently
beta-reduce-insistently.
None.
Single-inference.
This command is equivalent to disabling all
quasi-constructors and then calling beta-reduce.
:
beta-reduce
insistent-direct-inference
simplify-insistently
There is rarely any need to use this
command. It has the disagreeable effect of exploding
quasi-constructors.
beta-reduce-repeatedly
beta-reduce-repeatedly.
None.
Single-inference.
This command
attempts to beta-reduce each lambda-application in the assertion of
the given sequent repeatedly until there are no longer any
lambda-applications that beta-reduce.
:
beta-reduce
beta-reduce-antecedent
Since beta-reduction can often be applied
several times in a row, this command is usually preferable to the
command beta-reduce.
C-c b
beta-reduce-with-minor-premises
beta-reduce-with-minor-premises.
None.
Single-inference.
This command is the same as beta-reduce except that, instead of failing when convergence requirements
are not verified, it posts the unverified convergence requirements as
additional subgoals to be proved.
:
beta-reduce
simplify-with-minor-premises
This command
is useful for determining why a lambda-application does not
beta-reduce.
case-split
(case-split
list-of-formulas).
- First formula:
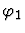 .
.
- Next formula (<RET> if done):
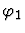 .
.
- Next formula (<RET> if done):
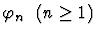 .
.
This command considers all the
different possible cases for
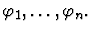
Notes:
- For each
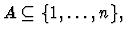
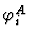 is
is 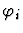 if
if 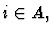 and
and
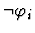 otherwise.
otherwise.
case-split-on-conditionals
(case-split-on-conditionals
occurrences). occurrences is a list of integers.
- Occurrences of conditionals to be raised (0-based):
A list l given in the form
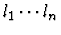 .
.
Multi-inference.
This command applies case-split to the first components of the conditional expressions in
the given sequent specified by l. The command simplify is
then applied to each of the newly created sequents.
:
case-split
raise-conditional
Avoid using this command with more than
two occurrences of conditionals.
choice-principle
choice-principle.
None.
Single-inference.
This command implements a version of
the axiom of choice.
| Conclusion |
![$\Gamma \Rightarrow
\exists f\mbox{:}[\sigma_1,\ldots,\sigma_n,\tau],
\forall x_1\mbox{:}\sigma^{\prime}_{1},\ldots,
x_n\mbox{:}\sigma^{\prime}_{n}, \varphi$](img651.gif) |
| Premise |
![$\Gamma \Rightarrow
\forall x_1\mbox{:}\sigma^{\prime}_{1},\ldots,
x_n\mbox{:...
..._{n},
\exists y_f\mbox{:}\tau,
\varphi[{y_f}/{f(x_1,\ldots,x_n)}]_{\rm all}$](img652.gif) |
Notes:
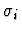 and
and
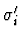 have the same type for all
i with
have the same type for all
i with
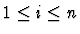 .
.
- The command fails if there is any occurrence of f in
 which is not in an application of the form
which is not in an application of the form
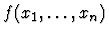 .
.
The existential sequence is often
introduced into the deduction graph using cut-with-single-formula.
contrapose
(contrapose
assumption). assumption can be given as an integer
i or a string 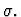
- 0-based index of antecedent-formula: i. If there is only
one assumption, this argument request is omitted.
Single-inference.
This command interchanges the
given sequent's assertion and its assumption given by i.
| Conclusion |
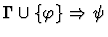 |
| Premise |
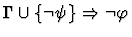 |
Notes:
- The index of
 in context
in context
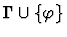 is i.
is i.
Use
contrapose if you want to do ``proof by contradiction.''
However, if there is nothing to contrapose with (because the sequent
has no assumptions), you will have to add an assumption by using cut-with-single-formula or instantiate-theorem.
c
cut-using-sequent
(cut-using-sequent
sequent-node). sequent-node can be given as an
integer (referring to the sequent node with that number) or as a list
(context-string assertion-string).
- Major premise number: The number of a sequent node.
Single-inference.
This command allows you to add some new
assumptions to the context of the given sequent. Of course, you are
required to show separately that the new assumptions are consequences
of the context. The node containing the major premise sequent must
exist before the command can be called. Usually you create this
sequent node with edit-and-post-sequent-node.
| Conclusion |
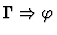 |
| Major Premise |
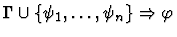 |
Minor Premises
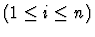 |
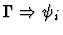 |
cut-with-single-formula.
To cut with one formula, you should usually
use cut-with-single-formula.
cut-with-single-formula
(cut-with-single-formula
formula).
- Formula to cut: String specifying a formula
 .
.
Single-inference.
This command allows you to add a new
assumption to the context of the given sequent. Of course, you are
required to show separately that the new assumption is a consequence
of the context.
| Conclusion |
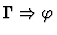 |
| Major Premise |
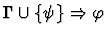 |
| Minor Premise |
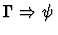 |
cut-using-sequent.
To cut with several formulas at the same
time, use cut-using-sequent.
&
definedness
definedness.
None.
Single-inference.
This command applies to a sequent
whose assertion is a definedness statement of the form
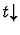 .
The command first tests whether the context entails the definedness of
t. If the test fails, the command then tries to reduce the sequent
to a set of simpler sequents.
.
The command first tests whether the context entails the definedness of
t. If the test fails, the command then tries to reduce the sequent
to a set of simpler sequents.
sort-definedness.
This command is mainly useful when t is
an application or a conditional.
direct-and-antecedent-inference-strategy
direct-and-antecedent-inference-strategy.
None.
Multi-inference.
This command repeatedly applies (1)
direct-inference to the given sequent and resulting sequents and
(2) antecedent-inference to newly created antecedents of the
given sequent and resulting sequents until no more such direct and
antecedent inferences are possible.
:
antecedent-inference-strategy
direct-and-antecedent-inference-strategy-with-simplification
direct-inference-strategy
D
:
direct-and-antecedent-inference-strategy-with-simplification.
None.
Multi-inference.
This command first applies direct-and-antecedent-inference-strategy to the given sequent, and
then applies simplify to all resulting sequents.
:
antecedent-inference-strategy
direct-and-antecedent-inference-strategy
direct-inference-strategy
direct-inference
direct-inference.
None.
Single-inference.
This command applies an analogue of an
introduction rule of Gentzen's sequent calculus (in reverse), based on
the leading constructor of the assertion of the given sequent.
| Conclusion |
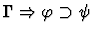 |
| Premise |
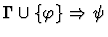 |
| Conclusion |
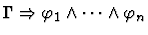 |
Premises
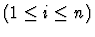 |
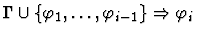 |
| Conclusion |
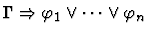 |
| Premise |
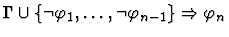 |
| Conclusion |
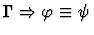 |
| Premises |
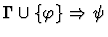 |
| |
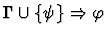 |
| Conclusion |
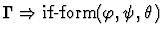 |
| Premises |
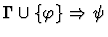 |
| |
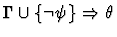 |
| Conclusion |
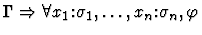 |
| Premise |
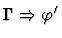 |
Notes:
-
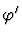 is obtained from
is obtained from  by renaming the
variables among
by renaming the
variables among
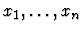 which are free in both
which are free in both  and
the context
and
the context 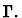
:
antecedent-inference
direct-inference-strategy
unordered-direct-inference
Keep in mind that any direct inference
produces subgoals which together are equivalent to the original goal.
Thus it is always safe to do direct inferences, in the sense that they
do not produce false subgoals from true goals.
d
direct-inference-strategy
direct-inference-strategy.
None.
Multi-inference.
This command repeatedly applies direct-inference to the given sequent and resulting sequents
until no more direct inferences are possible. In other words, it adds
to the deduction graph the smallest set of sequents containing the
given sequent and closed under direct inferences.
:
antecedent-inference-strategy
direct-inference
direct-and-antecedent-inference-strategy
disable-quasi-constructor
(disable-quasi-constructor
quasi-constructor).
- Quasi-constructor name: The name of a quasi-constructor
in the expression.
Null-inference.
This command disables the
quasi-constructor given as argument.
edit-and-post-sequent-node
(edit-and-post-sequent-node
context-string assertion-string).
- Edit sequent and C-c C-c when finished. A sequent
presented as a string of formulas using => to separate the
sequent assumptions from the sequent assertion.
Null-inference.
This commands adds the sequent given
as an argument to the deduction graph.
e
eliminate-defined-iota-expression
(eliminate-iota
index symbol).
- 0-based index of iota-expression occurrence: i.
- Name of replacement variable: y
Multi-inference.
This command replaces the i-th
occurrence of an iota-expression in the given sequent's assertion with
the variable y. The command is predicated upon the iota-expression
being defined with respect to the sequent's context. (An iota-expression is an expression whose lead constructor is iota or a quasi-constructor that builds an iota-expression.)
| Conclusion |
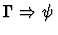 |
| Major Premise |
![$\Gamma \cup
\{\varphi[{y}/{x}]_{\rm free},
\forall z\mbox{:}\sigma, (\varphi[{z}/{x}]_{\rm free}
\supset z=y)\}
\Rightarrow \psi'$](img671.gif) |
| Minor Premise |
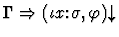 |
Notes:
-
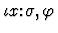 is the i-th
iota-expression occurrence in
is the i-th
iota-expression occurrence in  .
.
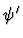 is the result of replacing the i-th iota
expression occurrence in
is the result of replacing the i-th iota
expression occurrence in  with y.
with y.
eliminate-iota.
This command is very useful for dealing
with iota-expressions that are known to be defined with respect to the
sequent's context. The minor premise is grounded automatically if the
sequent's context contains
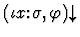 .
.
eliminate-iota
(eliminate-iota index).
- 0-based index of iota-expression occurrence: i.
Single-inference.
This command applies to a sequent
whose assertion is an atomic formula or negated atomic formula
containing a specified occurrence of an iota-expression. The command
reduces the sequent to an equivalent sequent in which the specified
iota-expression occurrence is ``eliminated.'' (An iota-expression is an expression whose lead constructor is iota or a quasi-constructor that builds an iota-expression.)
| Conclusion |
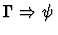 |
| Major Premise |
![$\Gamma \Rightarrow \exists y\mbox{:}\sigma,
(\varphi[{y}/{x}]_{\rm free} \wed...
...rall z\mbox{:}\sigma, (\varphi[{z}/{x}]_{\rm free}
\supset z=y) \wedge \psi')$](img676.gif) |
| Conclusion |
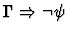 |
| Major Premise |
![$\Gamma \Rightarrow \exists y\mbox{:}\sigma,
(\varphi[{y}/{x}]_{\rm free} \wedge
\forall z\mbox{:}\sigma, (\varphi[{z}/{x}]_{\rm free}
\supset z=y)) \supset$](img678.gif) |
| |
![$\exists y\mbox{:}\sigma,
(\varphi[{y}/{x}]_{\rm free} \supset
\neg\psi')$](img679.gif) |
Notes:
 is an atomic formula.
is an atomic formula.
-
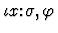 is the i-th iota-expression
occurrence in
is the i-th iota-expression
occurrence in  ,
an atomic formula.
,
an atomic formula.
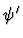 is the result of replacing the i-th iota-expression
occurrence in
is the result of replacing the i-th iota-expression
occurrence in  with y.
with y.
- The occurrence of
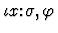 in
in
 is within some argument component s of
is within some argument component s of  .
Moreover, the
occurrence is an extended application component of s, where a is
an extended application component of b if either a is bor b is an application of kind
.
Moreover, the
occurrence is an extended application component of s, where a is
an extended application component of b if either a is bor b is an application of kind 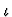 and a is an extended
application component of a component of b.
and a is an extended
application component of a component of b.
eliminate-defined-iota-expression.
If  is an equation or a definedness
expression, the macete eliminate-iota-macete is more direct than
eliminate-iota.
is an equation or a definedness
expression, the macete eliminate-iota-macete is more direct than
eliminate-iota.
enable-quasi-constructor
(enable-quasi-constructor
quasi-constructor).
- Quasi-constructor name: The name of a quasi-constructor
in the expression.
Null-inference.
This command enables the
quasi-constructor given as argument.
extensionality
extensionality.
None.
Single-inference.
If the sequent node assertion is an
equality or quasi-equality or the negation of an equality or
quasi-equality of n-ary functions, this command applies the
extensionality principle.
| Conclusion |
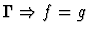 |
| Major Premise |
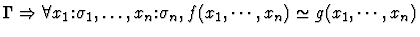 |
| Minor Premise |
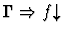 |
| Minor Premise |
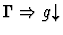 |
| Conclusion |
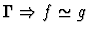 |
| Major Premise |
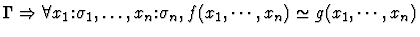 |
| Minor Premise |
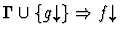 |
| Minor Premise |
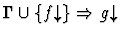 |
| Conclusion |
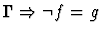 |
| Premise |
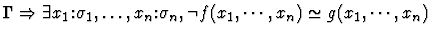 |
| Conclusion |
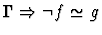 |
| Premise |
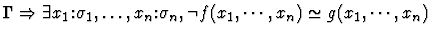 |
Notes:
- If the sorts of f and g are
![$[\alpha_1,\ldots,\alpha_n,\alpha_{n+1}]$](img95.gif) and
and
![$[\beta_1,\ldots,\beta_n,\beta_{n+1}]$](img690.gif) ,
respectively, then
,
respectively, then
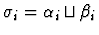 for all i with
for all i with
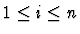 .
.
- A sequent node corresponding to a minor premise is not
created if the truth of the minor premise is immediately apparent to
IMPS.
- If f and g are of kind
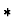 ,
then ``='' is used in
place of ``
,
then ``='' is used in
place of ``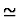 '' in the premise.
'' in the premise.
By substitution of quasi-equals for
quasi-equals, both f=g and
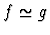 imply
imply
So in this direction extensionality is nothing new.
~
force-substitution
(force-substitution
expression replacement occurrences). expression and
replacement are denoted by strings, and occurrences is a
list of integers.
- Expression to replace: The subexpression e of the sequent
node assertion you want to replace.
- Replace it with: The new expression r you want to replace it
with.
- 0-based indices of occurrences to change: A list lgiven in the form
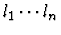 .
.
Single-inference.
This command allows you to change
part of the sequent assertion. It yields two or more new subgoals. One
subgoal is obtained from the original sequent assertion by making the
requested replacements. The other subgoals assert that the
replacements are sound.
| Conclusion |
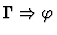 |
| Major Premise |
![$\Gamma \Rightarrow \varphi[{r}/{e}]_{l}$](img694.gif) |
Minor Premises
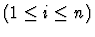 |
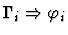 |
Notes:
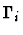 is the local context of
is the local context of
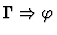 at
the location of the li-th occurrence of e in
at
the location of the li-th occurrence of e in  .
.
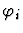 is
is
-
 if e is a formula and the parity of the path li is
0.
if e is a formula and the parity of the path li is
0.
-
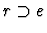 if e is a formula and the parity of the path
li is 1.
if e is a formula and the parity of the path
li is 1.
-
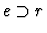 if e is a formula and the parity of the path li is -1.
if e is a formula and the parity of the path li is -1.
-
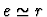 in all other cases.
in all other cases.
f
generalize-using-sequent
(generalize-using-sequent
major-premise). major-premise can be given as an
integer (referring to the sequent node with that number) or as a list
(context-string assertion-string).
- Major premise number: The number of a sequent node.
Single-inference.
This command generalizes the
assertion of the given sequent. The node containing the major premise
sequent must exist before the command can be called. Usually you
create this sequent node with edit-and-post-sequent-node.
| Conclusion |
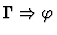 |
| Major Premise |
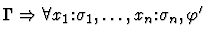 |
Minor Premises
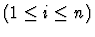 |
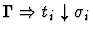 |
Notes:
 is the result of simultaneously
replacing each free occurrence of xi in
is the result of simultaneously
replacing each free occurrence of xi in 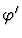 with ti for
all i with
with ti for
all i with
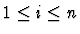 .
.
- ti is free for xi in
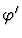 for each i with
for each i with
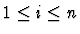 .
.
incorporate-antecedent
(incorporate-antecedent
assumption). assumption can be given as an integer
i or a string 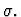
- 0-based index of antecedent-formula: i. If there is only
one assumption, this argument request is omitted.
Single-inference.
This commands does the reverse
of direct-inference on an implication.
| Conclusion |
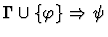 |
| Premise |
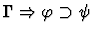 |
Notes:
- The index of
 in the context
in the context
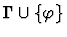 is i.
is i.
direct-inference.
This command is used for incorporating
an assumption of a sequent's context into the sequent's assertion. It
is particularly useful as a preparation for applying such commands as
apply-macete, beta-reduce, and simplify.
@
induction
(induction
inductor variable). inductor is a symbol
naming an inductor, and variable is a string or (). If
() is supplied as argument, IMPS will choose the variable of
induction itself.
- Inductor: An inductor is an IMPS structure which
has an associated induction principle together with heuristics (in the
form of macetes and commands) to handle separately the base and
induction cases.
- Variable to induct on (<RET> to use IMPS
default): IMPS will choose a variable of the appropriate sort to
induct on. Thus, in general, there is no danger that it will attempt to
induct on a variable for which induction makes no sense. However, if
various choices for an induction variable are possible, the choice is
more or less arbitrary. In these cases, you should be prepared to
suggest the variable.
Multi-inference.
This command attempts to apply a
formula called an induction principle to a sequent and applies
some auxiliary inferences as well. The induction principle used by
IMPS is determined by the inductor you give as an argument. When
using the induction command, the system will attempt to reformulate the
sequent in a form which matches the induction principle. In
particular, you can use the induction command directly in cases where
the goal sequent does not exactly match the induction principle.
In a formal sense ``induction'' refers to
an axiom or theorem in a particular theory (for example, the formula
of weak induction below), and in this sense, ``applying
induction,'' means applying this formula to a sequent. However,
induction alone rarely gets the job done. Other tricks, such as
algebraic simplification, beta-reduction, and unfolding of definitions,
especially recursive ones, are usually needed. In this broader sense,
induction can be thought of as a proof technique incorporating a large
number of fairly standard inferences.
Despite its simplicity, induction is one of the most powerful proof
techniques in mathematics, especially in proofs for formulas involving
the integers. Moreover, forms of induction are also used in theories
of syntax or theories of lists. An induction principle in one of these
theories is usually referred to as structural induction.
The induction principle for the inductor integer-inductor is the
formula
This formula is usually referred to as the principle of weak
induction. You might also be familiar with the principle of
strong induction; in fact, both induction principles are equivalent.
However, some formulas cannot be proved directly with the
principle of weak induction, because the induction hypothesis is not
sufficiently strong to prove the induction conclusion. In such cases,
instead of using a different induction principle, you first prove a
stronger formula by using the same weak induction principle.
You can build inductors using the form def-inductor. See
Section 17.1.
i
insistent-direct-inference
insistent-direct-inference.
None.
Single-inference.
This command is equivalent to disabling all
quasi-constructors and then calling direct-inference.
:
direct-inference
insistent-direct-inference-strategy.
There is rarely any need to use this
command. It has the disagreeable effect of exploding
quasi-constructors.
insistent-direct-inference-strategy
insistent-direct-inference-strategy.
None.
Multi-inference.
This command repeatedly applies the
insistent-direct-inference command to the goal node and
resulting subgoal nodes until no more insistent direct inferences are
possible. In other words, it adds to the deduction graph the smallest
set of sequents containing the goal sequent and closed under insistent
direct inferences. This command is equivalent to disabling all
quasi-constructors and then calling direct-inference-strategy.
:
direct-inference-strategy
insistent-direct-inference
Like insistent-direct-inference,
this command has the disagreeable effect of exploding
quasi-constructors.
instantiate-existential
(instantiate-existential
instantiations). instantiations is a list of
strings denoting expressions.
- Instance for variable x1 of sort
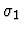 :
t1.
:
t1.
- Instance for variable xn of sort
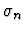 :
tn
:
tn
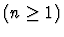 .
.
Multi-inference.
This command instantiates an
existential assertion with the specified terms.
| Conclusion |
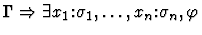 |
| Major Premise |
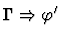 |
Minor Premises
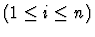 |
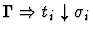 |
Notes:
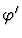 is the result of simultaneously
replacing each free occurrence of x1 in
is the result of simultaneously
replacing each free occurrence of x1 in  with ti, for
each i with
with ti, for
each i with
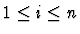 ,
if necessary renaming bound variables
in
,
if necessary renaming bound variables
in  to avoid variable captures.
to avoid variable captures.
auto-instantiate-existential.
instantiate-theorem
(instantiate-theorem
theorem instantiations). theorem is the name of a
theorem, and instantiations is a list of strings denoting
expressions.
- Theorem name: The name of a theorem
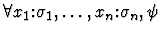 in the deduction
graph's theory.
in the deduction
graph's theory.
- Instance for variable x1 of sort
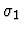 :
t1.
:
t1.
- Instance for variable xn of sort
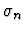 :
tn
:
tn
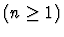 .
.
Multi-inference.
This command instantiates the
argument theorem with the specified terms
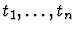 and
then adds the resulting formula to the context of the given sequent.
and
then adds the resulting formula to the context of the given sequent.
| Conclusion |
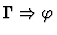 |
| Major Premise |
 |
Minor Premises
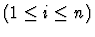 |
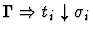 |
Notes:
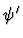 is the result of simultaneously
replacing each free occurrence of xi in
is the result of simultaneously
replacing each free occurrence of xi in  with ti, for each
i with
with ti, for each
i with
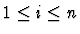 ,
if necessary renaming bound variables in
,
if necessary renaming bound variables in
 to avoid variable captures.
to avoid variable captures.
:
assume-theorem
instantiate-transported-theorem
instantiate-transported-theorem
(instantiate-transported-theorem theorem interpretation
instantiations). theorem is the name of a theorem, interpretation is the name of a theory interpretation, and instantiations is a list of strings denoting expressions.
- Theorem name: The name of a theorem
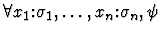 in T.
in T.
- Theory interpretation (<RET> to let IMPS find one):
The
name of a theory interpretation i of T in the deduction
graph's theory.
- Instance for variable x1 of sort
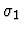 :
t1.
:
t1.
- Instance for variable xn of sort
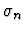 :
tn
:
tn
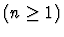 .
.
Multi-inference.
This command transports the argument
theorem to the deduction graph's theory via i. Then, the
transported theorem is instantiated with the specified terms
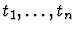 .
And, finally, the resulting formula is added to the
context of the given sequent.
.
And, finally, the resulting formula is added to the
context of the given sequent.
If no theory interpretation name is given, IMPS will try to find a
theory interpretation to play the role of i using the
sort information contained in the terms
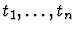 .
.
:
assume-transported-theorem
instantiate-theorem
IMPS can often find an appropriate
theory interpretation automatically when the home theory of the
theorem is a generic theory, i.e., a theory which contains neither
constants nor axioms.
instantiate-universal-antecedent
(instantiate-universal-antecedent assumption instantiations). assumption can be given as an integer
i or a string 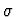 ,
and instantiations is a list of strings
denoting expressions.
,
and instantiations is a list of strings
denoting expressions.
- 0-based index of universal antecedent formula
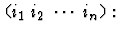 i. The
i. The
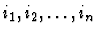 are
the indices of the universal assumptions of the sequent node. In case
there is only one universal antecedent formula, this argument request
is omitted.
are
the indices of the universal assumptions of the sequent node. In case
there is only one universal antecedent formula, this argument request
is omitted.
- Instance for variable x1 of sort
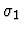 :
t1.
:
t1.
- Instance for variable xn of sort
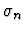 :
tn
:
tn
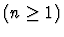 .
.
Multi-inference.
This command instantiates the i-th
assumption of the context of the given sequent (provided the
assumption is a universal statement).
| Conclusion |
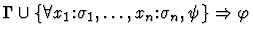 |
| Major Premise |
 |
Minor Premises
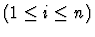 |
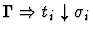 |
Notes:
- The index of the assumption
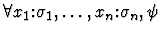 in the context
in the context
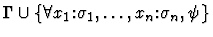 is i.
is i.
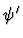 is the result of simultaneously
replacing each free occurrence of x1 in
is the result of simultaneously
replacing each free occurrence of x1 in  with ti, for each
i with
with ti, for each
i with
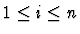 ,
if necessary renaming bound variables in
,
if necessary renaming bound variables in
 to avoid variable captures.
to avoid variable captures.
:
auto-instantiate-universal-antecedent
instantiate-universal-antecedent-multiply
instantiate-universal-antecedent-multiply
(instantiate-universal-antecedent-multiply assumption lists-of-instantiations). assumption can be given as an
integer i or a string 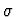 ,
and lists-of-instantiations is
a list of lists of strings which specify the expressions that
instantiate the universally quantified assumption.
,
and lists-of-instantiations is
a list of lists of strings which specify the expressions that
instantiate the universally quantified assumption.
- 0-based index of antecedent-formula: i. If there is only
one assumption, this argument request is omitted.
- First instance term: t1.
- Next instance term (<RET> if done): t2.
- Next instance term (<RET> if done):
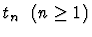 .
.
- Input terms for another instance? (y or n)
Multi-inference.
This command produces one or more
instances of the i-th assumption of the context of the given sequent
(provided the assumption is a universal statement) in the same way
that instantiate-universal-antecedent produces one instance
of the assumption.
:
auto-instantiate-universal-antecedent
instantiate-universal-antecedent
prove-by-logic-and-simplification
(prove-by-logic-and-simplification persistence).
- Backchaining persistence: An integer, which is 3 by default.
Multi-inference.
This command tries to ground a
sequent by applying a list inference procedures (some of which have a
sequent assumption as an additional argument) to the goal node and
recursively to the generated subgoal nodes. See
Table 18.1. When an inference procedure is applied to
the goal sequent or to a subgoal sequent, two possibilities can occur:
- 1.
- The
inference procedure fails. In this case, prove-by-logic-and-simplification tries the same
inference procedure with the next assumption as argument (if this
makes sense), the next inference procedure on the list, if one exists,
or otherwise backtracks.
- 2.
- The inference procedure succeeds, either grounding the node or
generating one or more new subgoals to prove. In this case we attempt
to prove each new subgoal by applying the primitive inferences in order.
Table 18.1:
Search Order for prove-by-logic-and-simplification
| Condition |
Procedure |
Action |
| do-simplify? |
simplify |
lower do-simplify? |
| 0< persist |
backchain-through-formula |
lower persist |
| |
|
raise do-simplify? |
| |
antecedent-inference for |
|
| |
existentials and conjunctions |
|
| |
direct-inference |
|
| |
antecedent-inference for |
|
| |
other assumptions |
raise do-simplify? |
| 0< persist |
backchain-inference |
|
| |
sort-definedness |
|
| |
definedness |
|
| |
extensionality |
raise do-simplify? |
| |
conditional-inference followed |
raise do-simplify? |
| |
by direct-inference |
|
Notes:
- 1.
- The variable persist is the backchaining persistence supplied
as an argument to the command. lower persist means reduce
backchaining persistence by 1.
- 2.
- do-simplify? is a boolean flag which starts off as true when the command is called.
|
This command is an example of an ending
strategy, that is, a proof construction procedure to be used when all
that remains to be done is completely straightforward reasoning. It
should be used with great caution since in the cases in which it fails
to ground a node it may generate a large number of irrelevant
subgoals.
None, lest you accidently hit it.
raise-conditional
(raise-conditional
occurrences). occurrences is given by a list of
integers.
- Occurrences of conditionals to be raised (0-based):
A list l given in the form
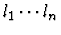 .
.
Single-inference.
This command will ``raise'' a subset
of the conditional expressions (i.e., expressions whose lead
constructor is if), specified by l, in the assertion of
the given sequent
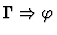 .
.
For the moment, let us assume that n=1. Suppose the l1-th
occurrence of a conditional expression in  is the a-th
occurrence of
is the a-th
occurrence of
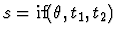 in
in  ;
the smallest
formula containing the a-th occurrence of s in
;
the smallest
formula containing the a-th occurrence of s in  is the
b-th occurrence of
is the
b-th occurrence of  in
in  ;
and the a-th occurrence of
s in
;
and the a-th occurrence of
s in  is the c-th occurrence of s in
is the c-th occurrence of s in  .
If every
free occurrence of a variable in s is also a free occurrence in
.
If every
free occurrence of a variable in s is also a free occurrence in
 ,
the command reduces the sequent to
,
the command reduces the sequent to
and otherwise the command fails.
Now assume n > 1. The command will then simultaneously raise each
specified occurrence of a conditional expression in  ,
in the
manner of the previous paragraph, if there are no conflicts between
the occurrences. The kinds of conflicts that can arise and how they
are resolved are listed below:
,
in the
manner of the previous paragraph, if there are no conflicts between
the occurrences. The kinds of conflicts that can arise and how they
are resolved are listed below:
- If two or more specified occurrences of a conditional expression
s in
 are contained in same smallest formula, they are
raised together.
are contained in same smallest formula, they are
raised together.
- If two or more specified occurrences of distinct conditional
expressions in
 are contained in same smallest formula, at
most one of the occurrences is raised.
are contained in same smallest formula, at
most one of the occurrences is raised.
- If
 and
and 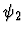 are the smallest formulas
respectively containing two specified occurrences of a conditional
expression in
are the smallest formulas
respectively containing two specified occurrences of a conditional
expression in  and
and  is a proper subexpression of
is a proper subexpression of
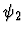 ,
then the first specified conditional expression is not
raised.
,
then the first specified conditional expression is not
raised.
case-split-on-conditionals.
This command can be used to change a
conditional expression
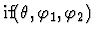 in a
sequent's assertion, where
in a
sequent's assertion, where 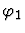 and
and 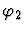 are formulas, to
the conditional formula
are formulas, to
the conditional formula
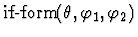 .
.
r
simplify
simplify.
None.
Single-inference.
This command simplifies the
assertion of the given sequent with respect to the context of the
sequent. It uses both theory-specific and general logical methods to
reduce the sequent to a logically equivalent sequent. The
theory-specific methods include algebraic simplification, deciding
rational linear inequalities, and applying rewrite rules.
:
beta-reduce
simplify-antecedent
simplify-insistently
simplify-with-minor-premises
This is a very powerful command that can be
computationally expensive. Computation can often be saved by using
the weaker command beta-reduce.
C-c s
simplify-antecedent
(simplify-antecedent
assumption). assumption can be given as an integer
i or a string 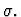
- 0-based index of antecedent-formula: i. If there is only
one assumption, this argument request is omitted.
Multi-inference.
This command is used for simplifying
an assumption in the context of the given sequent with respect to this
context. It is equivalent to the following sequence of commands: contrapose applied to the given sequent with argument i; simplify applied to the sequent yielded by the previous command; and
contrapose applied to the sequent yielded by the previous
command with the index of the negated assertion of the original
sequent. The commands halts if simplify grounds the first
produced sequent.
:
beta-reduce-antecedent
simplify
simplify-insistently
simplify-insistently.
None.
Single-inference.
This command is equivalent to disabling all
quasi-constructors and then calling simplify.
:
beta-reduce-insistently
insistent-direct-inference
simplify
There is rarely any need to use this
command. It has the disagreeable effect of exploding
quasi-constructors.
simplify-with-minor-premises
simplify-with-minor-premises.
None.
Single-inference.
This command is the same as simplify except that, instead of failing when convergence requirements
are not verified, it posts the unverified convergence requirements as
additional subgoals to be proved.
:
beta-reduce-with-minor-premises
simplify
This command is useful for identifying
convergence requirements that the simplifier cannot verify.
sort-definedness
sort-definedness.
None.
Single-inference.
This command applies to a sequent
whose assertion is a definedness statement of the form
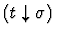 .
The command first tests whether the context
entails the definedness of t in
.
The command first tests whether the context
entails the definedness of t in 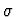 .
If the test fails, the
command then tries to reduce the sequent to a set of simpler sequents.
In particular, when t is a conditional term if
.
If the test fails, the
command then tries to reduce the sequent to a set of simpler sequents.
In particular, when t is a conditional term if
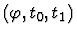 ,
it distributes the sort definedness assertion into the
consequent and alternative. If t0 and t1 are not themselves
conditional terms, the new subgoal has the assertion
if-form
,
it distributes the sort definedness assertion into the
consequent and alternative. If t0 and t1 are not themselves
conditional terms, the new subgoal has the assertion
if-form
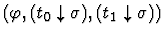 .
If
one or both of them is a conditional term, then the sort definedness
assertion is recursively distributed into the consequents and
alternatives.
.
If
one or both of them is a conditional term, then the sort definedness
assertion is recursively distributed into the consequents and
alternatives.
definedness.
This command is mainly useful when t is
an application, a function, or a conditional term.
sort-definedness-and-conditionals
None.
Multi-inference.
This strategy invokes sort-definedness.
Insistent direct inference and repeated beta reduction are then
invoked, followed by case-split-on-conditionals, applied to the first
conditional term.
sort-definedness.
This command is useful for a goal
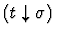 when the definition of
when the definition of 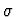 involves a conditional
term.
involves a conditional
term.
unfold-defined-constants
unfold-defined-constants.
None.
Multi-inference.
This command replaces every
occurrence of a defined constant by its respective unfolding. The
command beta-reduce-repeatedly is called after all the
unfoldings are performed.
:
unfold-defined-constants-repeatedly
unfold-directly-defined-constants
unfold-recursively-defined-constants
unfold-single-defined-constant
C-c u
unfold-defined-constants-repeatedly
unfold-defined-constants-repeatedly.
None.
Multi-inference.
This command replaces every
occurrence of a defined constant by its respective unfolding,
repeatedly, until there are no occurrences of defined constants.
The command beta-reduce-repeatedly is called after all the
unfoldings are performed.
:
unfold-defined-constants
unfold-directly-defined-constants-repeatedly
unfold-recursively-defined-constants-repeatedly
unfold-single-defined-constant
If there are occurrences of recursively
defined constants, this command can run forever.
unfold-directly-defined-constants
unfold-directly-defined-constants.
None.
Multi-inference.
This command replaces every
occurrence of a directly defined constant by its respective unfolding.
(A directly defined constant is a constant defined
nonrecursively.) The command beta-reduce-repeatedly is called
after all the unfoldings are performed.
:
unfold-defined-constants
unfold-directly-defined-constants-repeatedly
unfold-recursively-defined-constants
unfold-single-defined-constant
unfold-directly-defined-constants-repeatedly
unfold-directly-defined-constants-repeatedly.
None.
Multi-inference.
This command replaces every
occurrence of a directly defined constant by its respective unfolding,
repeatedly, until there are no occurrences of directly defined
constants. (A directly defined constant is a constant defined
nonrecursively.) The command beta-reduce-repeatedly is called
after all the unfoldings are performed.
:
unfold-defined-constants-repeatedly
unfold-directly-defined-constants
unfold-recursively-defined-constants-repeatedly
unfold-single-defined-constant
This command will
always terminate, unlike
unfold-defined-constants-repeatedly
and
unfold-recursively-defined-constants-repeatedly.
unfold-recursively-defined-constants
unfold-recursively-defined-constants.
None.
Multi-inference.
This command
replaces every occurrence of a recursively defined constant by its
respective unfolding. The command beta-reduce-repeatedly is
called after all the unfoldings are performed.
:
unfold-defined-constants
unfold-directly-defined-constants
unfold-recursively-defined-constants-repeatedly
unfold-single-defined-constant
unfold-recursively-defined-constants-repeatedly
unfold-recursively-defined-constants-repeatedly.
None.
Multi-inference.
This command
replaces every occurrence of a recursively defined constant by its
respective unfolding, repeatedly, until there are no occurrences of
recursively defined constants. The command beta-reduce-repeatedly is called after all the unfoldings are
performed.
:
unfold-defined-constants-repeatedly
unfold-directly-defined-constants-repeatedly
unfold-recursively-defined-constants
unfold-single-defined-constant
This command may run forever.
unfold-single-defined-constant
(unfold-single-defined-constant occurrences constant). occurrences is a list of integers, and constant is
denoted by the constant name.
- Constant name: c.
- Occurrences to unfold (0-based): A list l given
in the form
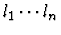 .
.
Notice that the order in which arguments are requested is different
than the order for script usage.
Multi-inference.
This command replaces each specified
occurrence of the defined constant c by its unfolding e:
| Conclusion |
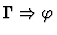 |
| Premise |
![$\Gamma \Rightarrow \varphi[{e}/{c}]_{l}$](img722.gif) |
The command beta-reduce-repeatedly is called
after all the unfoldings are performed.
:
unfold-defined-constants
unfold-defined-constants-repeatedly
unfold-directly-defined-constants
unfold-directly-defined-constants-repeatedly
unfold-recursively-defined-constants
unfold-recursively-defined-constants-repeatedly
unfold-single-defined-constant-globally
The related commands are all elaborations
of this command.
u
unfold-single-defined-constant-globally
(unfold-single-defined-constant-globally constant).
Multi-inference.
This command replaces every
occurrence of the defined constant c by its unfolding e:
| Conclusion |
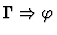 |
| Premise |
![$\Gamma \Rightarrow \varphi[{e}/{c}]_{\rm all}$](img723.gif) |
The command beta-reduce-repeatedly is called
after all the unfoldings are performed.
unfold-single-defined-constant.
U
unordered-direct-inference
unordered-direct-inference.
None.
Single-inference.
If the sequent node assertion is a
conjunction, this command does a direct inference without
strengthening the context.
direct-inference.
weaken
(weaken
assumption-list). assumption-list can be given as a
list of numbers, a list of strings, or an assumption-list form.
- List of formula indices to omit (0-based): A list l given
in the form
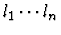 .
.
Single-inference.
This command removes one or more
assumptions you specify from the context of the given sequent.
| Conclusion |
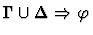 |
| Premise |
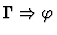 |
Notes:
- The indices of the members of
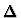 in the context
in the context
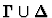 are given by l.
are given by l.
You might wonder why you would ever want
to remove an assumption, but in fact, in many cases this is a
natural step to take:
- If an assumption is irrelevant, then removing it will do no harm and
will make the job of the simplifier a lot easier,
- It is often the case that sequent nodes are identical except for the
addition of ``irrelevant'' assumptions. In this case, removing the
irrelevant assumptions allows you to ground both sequents by just
grounding one.
w



Next: 19. The Primitive Inference
Up: 3. Reference Manual
Previous: 17. The IMPS Special
System Administrator
2000-07-23
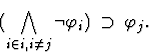
![\begin{eqnarray*}\lefteqn{\forall s\mbox{:}[{ \bf z },\ast] ,m\mbox{:}{ \bf z },...
... t \mbox{:}{ \bf z }, m \leq t \supset (s(t) \supset s(t+1)))).
\end{eqnarray*}](img703.gif)