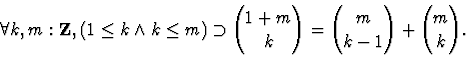


Next: Bibliography
Up: 3. Reference Manual
Previous: 20. The Initial Theory
20.0.0.0.1 Alpha-equivalence
Two expressions are
alpha-equivalent if one can be obtained from the other by renaming
bound variables.
20.0.0.0.2 Application
An expression whose lead constructor
is named apply. Applications must have at least two components. The
first component of an application is called the operator and the
remaining components are called arguments. Applications are
usually denoted by prefixing the operator to the arguments enclosed in
parentheses as
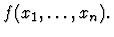 However, other forms (such as
infix for algebraic operations) are also used.
However, other forms (such as
infix for algebraic operations) are also used.
20.0.0.0.3 Beta-reduction
An inference rule which plugs in the
values of lambda-applications. For example, beta-reduction
transforms the expression
to 13.
20.0.0.0.4 Buffer
An Emacs data structure for representing
portions of text, for example, text files which are being edited. To
the user, a buffer has the appearance of a scrollable page. More than
one buffer may exist at a given time in an Emacs session. Users will
also use buffers to build, edit and evaluate def-forms.
20.0.0.0.5 Command form
An s-expression
used in proof scripts. The number and type of arguments is
command-dependent. If the command takes no arguments, then the form
command-name is also valid.
20.0.0.0.6 Compound expression
An expression with a
constructor and a (possibly empty) list of components. 1+2is a compound expression whose constructor is named apply and whose
components are +,1,2.
20.0.0.0.7 Constant
A kind of IMPS expression.
For example, in the theory named h-o-real-arithmetic, the expressions
1,2,+ are constants.
20.0.0.0.8 Constructor
One of the 19 logical constants of
LUTINS. Constructors are used to build compound
expressions.
20.0.0.0.9 Context
An IMPS data structure representing a set of
of formulas to be used as assumptions. Contexts contain various kinds
of cached information (for example, about definedness of terms), used
by the IMPS simplification machinery.
20.0.0.0.10 Core
All the basic logical and deductive machinery of
IMPS on which the soundness of the system depends.
20.0.0.0.11 Deduction graph
An IMPS data structure representing
a proof. Deduction graphs contain two kinds of nodes:
inference nodes and sequent nodes.
20.0.0.0.12 Def-form
An s-expression
whose evaluation has some effect on the IMPS environment, such as
building a theory, adding a theorem to a theory, making a definition
in a theory or building a translation between theories. There are
about 30 such def-forms.
20.0.0.0.13 Emacs
A text editor. Although various implementations
of Emacs exist, in this manual we mean exclusively GNU Emacs,
which is the extensible display editor developed by the Free Software
Foundation. Because of the many extension facilities it provides
(including a programming language with many string-processing
functions), GNU Emacs is well-suited for developing interfaces.
20.0.0.0.14 Expression
An IMPS data structure representing an
element of a language. Expressions are used to describe mathematical
entities or to make logical assertions. Two examples (printed in
TEX) are 22n-1 and
An expression is either a formal
symbol or a compound expression.
20.0.0.0.15 Evaluate
To cause an s-expression to be read by the
T process, thereby creating an internal representation of
a program, which is then executed by T. This sequence of
events usually has a number of side-effects on the IMPS environment.
For example, to define a constant named square in the theory
h-o-real-arithmetic, evaluate the s-expression:
(def-constant SQUARE
"lambda(x:rr, x^2)"
(theory h-o-real-arithmetic))
20.0.0.0.16 Formal symbol
A primitive IMPS expression. A formal
symbol has no components, although it is possible for an expression
with no components to be a compound expression. A formal symbol can
be a variable or a constant. Every formal symbol
has a name which is used for display. The name is a Lisp object
such as a symbol or a number.
20.0.0.0.17 Formula
Intuitively, an expression having a truth
value, for example,
In IMPS a formula is an expression whose sort is
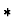 .
.
20.0.0.0.18 IMPS
A formal reasoning system and theorem prover
developed at The MITRE Corporation.
20.0.0.0.19 Inference node
A node in a deduction graph, connecting
a conclusion sequent node with zero or more hypothesis sequent nodes,
that represents an instance of a rule of inference.
20.0.0.0.20 Iota-expression
A compound expression whose lead
constructor is named iota, denoted in the mathematical syntax by
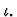 An iota-expression has the form
An iota-expression has the form
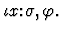 It denotes the unique object in the sort
It denotes the unique object in the sort 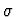 which
satisfies the condition
which
satisfies the condition 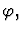 if such an object exists.
Otherwise, the iota-expression is undefined.
if such an object exists.
Otherwise, the iota-expression is undefined.
20.0.0.0.21 Kind
Each sort and expression is of kind 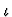 (also
written as iota) or
(also
written as iota) or 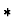 (prop). Expressions of kind
(prop). Expressions of kind 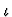 are
used to refer to mathematical objects; they may be undefined.
Expressions of kind
are
used to refer to mathematical objects; they may be undefined.
Expressions of kind 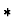 are primarily used in making assertions
about mathematical objects; they are always defined.
are primarily used in making assertions
about mathematical objects; they are always defined.
20.0.0.0.22 Lambda-application
An application whose
operator is a lambda-expression. For example
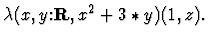
20.0.0.0.23 Lambda-expression
A compound expression whose lead
constructor is named lambda, denoted in the mathematical syntax
by  A lambda-expression has the form
A lambda-expression has the form
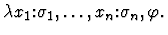 It
denotes the function of n arguments whose value at
It
denotes the function of n arguments whose value at
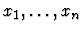 is given by the value of term
is given by the value of term 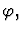 provided the xi are
of sort
provided the xi are
of sort 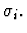
20.0.0.0.24 Language
Mathematically, a language in IMPS consists
of expressions, sorts, and user-supplied
information about sort inclusions. At the implementation level, a
language is a Lisp data structure having additional structure which
procedurally encodes this information. This is meant to facilitate
various kinds of lower level reasoning, such as reasoning about
membership of an expression in a sort.
20.0.0.0.25 Little theories
A version of the axiomatic method in
which mathematical reasoning is distributed over a network of theories
linked to one another by theory interpretations, in contrast to the
``big theory'' approach in which all reasoning is performed within a
single, usually very expressive theory.
20.0.0.0.26 Local context
The set of assumptions relevant to a
particular location in an expression.
20.0.0.0.27 LUTINS
A version of type theory with partial
functions and subtypes; the logic of IMPS.
20.0.0.0.28 Macete
A user-defined extension of the simplifier.
When a theorem is installed, it is also automatically installed as a
macete. The way the corresponding macete works depends on the
syntactic form of the theorem. In the simplest case in which the
theorem is a universally quantified equality, the theorem is used as a
rewrite rule. Macetes can be composed using the def-form
named def-compound-macete. The word ``macete'' comes from Brazilian
Portuguese, where it means ``clever trick.'' Theorem macetes can also
be made into
transportable macetes.
20.0.0.0.29 Mode Line
The line at the bottom of each buffer
window. It provides information about the displayed buffer such as its
name and mode.
20.0.0.0.30 Parser
A program which takes user input, usually
represented as text, and builds a data structure suitable for computer
processing.
20.0.0.0.31 Primitive inference procedure
An IMPS procedure that
implements one of the primitive rules of inference of the IMPS proof
system. IMPS has about 30 primitive inference procedures.
20.0.0.0.32 Proof
Conclusive mathematical evidence of
the validity of some assertion. The rules for admissible evidence are
given by a proof system.
20.0.0.0.33 Quasi-constructor
A user-defined macro/abbreviation
for building expressions. Quasi-constructors are used much like
constructors.
20.0.0.0.34 Quasi-equality
A quasi-constructor, written as infix
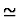 in the mathematical syntax.
in the mathematical syntax.
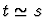 means that either
t and s are both undefined or they are equal.
means that either
t and s are both undefined or they are equal.
20.0.0.0.35 S-expression
The external representation of the basic
data structure of Lisp-like languages including T.
S-expressions are usually represented as nested lists such as
(fuba (abacaxi farofa) alface).
20.0.0.0.36 Sequent node
A node in a deduction graph that represents
a sequent, a formula composed of a set of assumptions and an
assertion.
20.0.0.0.37 Sort
A sort denotes a nonempty set of
mathematical entities. Every expression has a sort which
restricts the value of that expression.
20.0.0.0.38 Syntax
Rules for parsing and printing
expressions. The syntaxes that are currently used in
IMPS are the string syntax which allows for infix and postfix
notation, the s-expression syntax which provides a uniform prefix
syntax for all constructors and operators, and the tex
syntax for displaying (but not parsing) in TEX.
20.0.0.0.39 T
A dialect of Lisp developed at the Yale
University Computer Science Department in which the core machinery
of IMPS is implemented. T is very similar to the Scheme programming
language, familiar to readers of Abelson and Sussman's book
[1].
20.0.0.0.40 Tea
An alias for the T programming
language.
20.0.0.0.41 Theory
The term ``theory'' as used in this manual,
consists of a language and a set of closed formulas in the
language called axioms. A theory is implemented as a record
structure having slots for the language, the list of axioms, and other
relevant information. There is also a slot for a table of procedures
which the simplifier uses to apply the axioms. This is meant to
facilitate various kinds of lower-level reasoning, such as algebraic
or order simplification. In a different sense, theory is also
commonly used to refer to a collection of related facts about a given
mathematical structure, such as the theory of rings or the theory of
ordinary differential equations.
20.0.0.0.42 Theory ensemble
A data structure which bundles
together theories which are unions of copies of a single base theory.
Theory ensembles are mainly used to treat multiple instances of
structures, such as triples of metric spaces or pairs of vector
spaces.
20.0.0.0.43 Theory interpretation
A translation
that maps theorems to theorems.
20.0.0.0.44 Translation
An IMPS data structure, created with the
def-form named def-translation, that is used to
translate expressions from one theory to another.
20.0.0.0.45 Transportable macete
A theorem macete that can be
used in a theory different from the one in which it was installed. Transportable
macetes are named by the system by prefixing tr% to the name of the theorem.
20.0.0.0.46 Type
A sort that is maximal with respect to
the subsort relation.
20.0.0.0.47 Variable
A kind of IMPS expression.
An occurrence of a variable v within an expression is bound if it occurs
with the body of a binding constructor which includes v as a binding
variable. Otherwise, the occurrence of v is free.
20.0.0.0.48 Xview
An IMPS procedure for printing
expressions in TEX and then displaying them in an
X window TEX previewer.



Next: Bibliography
Up: 3. Reference Manual
Previous: 20. The Initial Theory
System Administrator
2000-07-23