20. The Initial Theory Library: An Overview

A theory library is a collection of theories, theory interpretations, and theory constituents (e.g., definitions and theorems) which serves as a database of mathematics. The basic unit of a theory library is a section; each section is a body of mathematics. Each section consists of a sequence of def-form specifications which are stored in a set of text files.

The IMPS initial theory library contains a large variety of basic mathematics. It is intended to provide you with a starting point for building your own theory library. It also is a source of examples that illustrates some of the diverse ways mathematics can be formulated in IMPS.

This chapter contains only a sampling of the sections that are contained in the IMPS initial theory library with a partial description of each section. Some of the descriptions contain a listing of the theories and some of the more important theorems and definitions included in that section.

Each section description begins with the symbol § followed by the section name. Each theory description begins with the symbol ¶ followed by the theory name.

   
§ abstract-calculus

The main theory of this section is normed-spaces. The section develops the basic notions of calculus (e.g., the derivative and the integral) in the context of normed spaces.

   
§ banach-fixed-point-theorem

This section has a proof of the Banach contractive mapping fixed point theorem, which states that any contractive mapping on a complete metric space has a unique fixed point.

   
§ basic-cardinality

This section introduces the basic notions of cardinality. It also proves some basic theorems about finite cardinality such as the fact that every subset of a finite set is itself finite.

   
§ basic-fields

The main theory of this section is fields. The section develops the machinery of field theory sufficiently for installing an algebraic processor for simplification.

   
§ basic-group-theory

This section contains two principle theories: groups and group-actions. The section includes a proof that the quotient of a group by a normal subgroup is itself a group. Also, several interpretations of group-actions in groups are defined.

   
§ basic-monoids

This section contains the theories monoid-theory and commutative-monoid-theory. In monoid-theory a constant monoid%prod is defined recursively as the iterated product of the primitive monoid operation. Basic properties of this constant are proved in monoid-theory and then are transported to theories with their own iterated product operators, such as h-o-real-arithmetic with the operators $\sum$ and $\prod$.

   
§ binary-relations

Binary relations are represented in this section as certain partial functions in the same way that sets are represented as indicators. Several basic operations on binary relations are formalized as quasi-constructors. As an exercise, the transitive closure of the union of two equivalence relations is shown to be an equivalence relation.

   
§ binomial-theorem

This section proves the combinatorial identity and the binomial theorem for fields.

   
§ counting-theorems-for-groups

This section contains a proof of the fundamental counting theorem for group theory. Several consequences of this theorem are proved including Lagrange's theorem.

   
§ foundation

This section is always loaded with IMPS. It contains the theory h-o-real-arithmetic and a number of definitions, theorems, and macetes in this theory. It also adds a number of definitions and theorems in the ``generic theories'' named generic-theory-1, generic-theory-2, generic-theory-3 and generic-theory-4 and the theory indicators.

Definitions

The following constants in h-o-real-arithmetic are among those included in the section foundation.

• sum (denoted $\sum$ in the mathematical syntax) is the least fixed point of the functional:
  
  $$\sigma \mapsto \lambda{m,n \mbox{:}{\bf Z} ,f \mbox{:}{\bf Z}... ...harpoonup {\bf R}}, \mbox{if}(m \leq n, \sigma(m,n-1,f)+f(n),0)$$
  
  

• prod (denoted $\prod$ in the mathematical syntax) is the least fixed point of the functional:
  
  $$\pi \mapsto \lambda{m,n \mbox{:}{\bf Z} ,f \mbox{:}{\bf Z} \r... ...rpoonup {\bf R}}, \mbox{if}(m \leq n, \pi(m,n-1,f) \, f(n),1)$$
  
  

• abs (denoted $\vert \cdot \vert$ in the mathematical notation) is
  
  $$\lambda{r \mbox{:}{\bf R}} ,\mbox{if}(0 \leq r,r,-r)$$
  
  

• floor: $\lambda x \mbox{:}{\bf R} , \iota z \mbox{:}{\bf Z}, z \leq x \wedge x<1+z$

   
§ groups-as-monoids

This section interprets monoid-theory in groups and then proves the telescoping product formula.

   
§ knaster-fixed-point-theorem

The main interest of this section is the statement and proof of the Knaster fixed point theorem which states that on a complete partial order with a least element and a greatest element, any monotone mapping has a fixed point. One important application of this result included in this section is a proof of the Schröder-Bernstein theorem.

   
§ metric-spaces

metric-spaces is the only new theory included in this section.

¶ metric-spaces

Contains h-o-real-arithmetic as a component theory.

Language

:

• Sorts: pp (P in the mathematical syntax) denotes the underlying set of points of the metric space.
• Constants: dist denotes a real-valued, two-place function on pp.

Axioms

:

1.

Positivity. $\forall x,y\mbox{:}{\bf P}, 0 \leq {\rm dist}(x,y)$

2.

Separation. $\forall x,y\mbox{:}{\bf P}, x=y \equiv {\rm dist}(x,y)=0$

3.

Symmetry. $\forall x,y\mbox{:}{\bf P}, {\rm dist}(x,y) = {\rm dist}(y,x)$

4.

Triangle Inequality. $\forall x,y,z\mbox{:}{\bf P}, {\rm dist}(x,z) \leq {\rm dist}(x,y)+{\rm dist}(y,z)$

   
§ metric-space-pairs

This section introduces the theory metric-space-pairs.

¶ metric-space-pairs

This theory is defined by the theory ensemble mechanism. Alternatively, it can be described as follows:

Language

: The language contains two copies of the language for metric spaces. Notice, however, that it does not contain two copies of the reals.

• Sorts:
  • pp_0 (${\bf P}_0$ in the mathematical syntax).
  • pp_1 (${\bf P}_1$ in the mathematical syntax).
• Constants:
  • dist_0 ( ${\rm dist}_0$ in the mathematical syntax).
  • dist_1 ( ${\rm dist}_1$ in the mathematical syntax).

Axioms

: The axioms are the positivity, separation, symmetry, and triangle inequality axioms for both functions dist_0 and dist_1. (See [13] for some example proofs.)

   
§ metric-space-continuity

This section develops continuity and related notions in the context of metric spaces.

   
§ number-theory

This section develops the rudiments of number theory. The fundamental theorem of arithmetic and the infinity of primes are proved.

   
§ pairs

A pair of elements a,b of sort $\alpha,\beta$ is represented as a function whose domain equals the singleton set $\{\langlea,b\rangle\}$. The basic operations on pairs are formalized as quasi-constructors.

   
§ partial-orders

This section contains the following theories:

• partial-order
• complete-partial-order

¶ partial-order

Language

:

• Base Types: uu (U in the mathematical syntax) denotes the underlying set of points.
• Constants: prec ($\prec$ in the mathematical syntax) denotes a binary relation on uu.

Axioms

:

• Transitivity. $\forall a,b,c \mbox{:}{\bf U}, a \prec b \wedge b \prec c \supset a \prec c$
• Reflexivity. $\forall a \mbox{:}{\bf U}, a \prec a$
• Anti-symmetry. $\forall a,b \mbox{:}{\bf U}, a \prec b \wedge b \prec a \supset a = b$

¶ complete-partial-order

Axioms

: In addition to the axioms for the theory partial-order, this theory has the completeness axiom which states that any nonempty set with an upper bound has a least upper bound. In a complete partial order it is also true that any nonempty set bounded below has a greatest lower bound.

   
§ pre-reals

Two IMPS theories of the real numbers are included in the pre-reals section:

• complete-ordered-field
• h-o-real-arithmetic

These theories are equivalent in the sense that each one can be interpreted in the other; moreover, the two interpretations compose to the identity. These interpretations are constructed in the section using the IMPS translation machinery.

¶ complete-ordered-field

In this theory, the real numbers are specified as a complete ordered field and the rational numbers and integers are specified as substructures of the real numbers. Exponentiation to an integer power is a defined constant denoting a partial function.

Language

:

• Sorts:
  • zz (Z in the mathematical syntax) denotes the set of integers.
  • qq (Q in the mathematical syntax) denotes the set of rational numbers.
  • rr (R in the mathematical syntax) denotes the set of real numbers.
• Constants:
  • + denotes real addition.
  • * (in the mathematical syntax, denoted by juxtaposition of its arguments) denotes rel multiplication.
  • - denotes sign negation.
  • / denotes division.
  • < denotes the binary predicate ``less than.''
  There are also an infinite number of constants, one for each rational number. Thus 8, [-9], [21/4] denote rational numbers.

Axioms

: The following is the list of all the axioms of the IMPS theory complete-ordered-field in the mathematical syntax.

1.

Trichotomy. $\forall y,x\mbox{:}{\bf R},x<y \vee x=y \vee y<x$

2.

Irreflexivity. $0 \not<0$

3.

Strict Positivity for Products. $\forall y,x\mbox{:}{\bf R}, 0<x \wedge 0<y \supset 0<x y$

4.

< Invariance . $\forall z,y,x\mbox{:}{\bf R},x<y \equiv x+z<y+z$

5.

Transitivity. $\forall z,y,x\mbox{:}{\bf R}, x<y \wedge y<z \supset x<z$

6.

Negative Characterization. $\forall x\mbox{:}{\bf R},x+(-x)=0$

7.

Characterization of 0. $\forall x\mbox{:}{\bf R},x+0=x$

8.

Associative Law for Multiplication. $\forall z,y,x\mbox{:}{\bf R},(x y) z=x (y z)$

9.

Left Distributive Law. $\forall z,y,x\mbox{:}{\bf R},x (y+z)=x y+x z$

10.

Multiplicative Identity. $\forall x\mbox{:}{\bf R},1 \, x=x$

11.

Commutative Law for Multiplication. $\forall y,x\mbox{:}{\bf R},x y=y x$

12.

Associative Law for Addition. $\forall z,y,x\mbox{:}{\bf R},(x+y)+z=x+(y+z)$

13.

Commutative Law for Addition. $\forall y,x\mbox{:}{\bf R},x+y=y+x$

14.

Characterization of Division. $\forall a,b\mbox{:}{\bf R}, b \neq 0 \supset b (a/b)=a$

15.

Division by Zero Undefined. $\forall a,b:ind,b=0 \supset \neg a/b \downarrow$

16.

Z Additive Closure. $\forall x,y:{\bf Z}, x+y \downarrow {\bf Z}$

17.

Z Negation Closure. $\forall x:{\bf Z}, -x \downarrow {\bf Z}$

18.

Induction.

$$\begin{array}{ll} &\forall s:{\bf Z} \rightarrow \ast, \for... ...orall t:{\bf Z},0<t \supset (s(t) \supset s(t+1))) \end{array}$$

19.

Characterization of [-1]. [-1]=-1

20.

Q is the field of fractions of Z. $\forall x\mbox{:}{\bf R}, x \downarrow {\bf Q} \equiv \exists a,b:{\bf Z},x=a/b$

21.

Order Completeness.

$$\begin{array}{l} \forall p\mbox{:}{\bf R} \rightarrow \ast, ... ...\gamma_1) \supset \gamma\leq \gamma_1 \end{array}\end{array}$$

¶ h-o-real-arithmetic

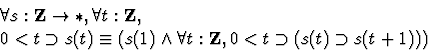
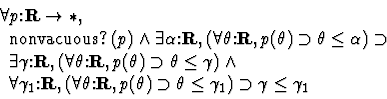
This is another axiomatization of the real numbers which we consider to be our working theory of the real numbers. The axioms of h-o-real-arithmetic include the axioms of complete-ordered-field, formulas characterizing exponentiation as a primitive constant and formulas which are theorems proven in complete-ordered-field. These theorems are needed for installing an algebraic processor and for utilizing the definedness machinery of the simplifier. The proofs of these theorems in the theory complete-ordered-field require a large number of intermediate results with little independent interest. The use of two equivalent axiomatizations frees our working theory of the reals from the burden of recording these uninteresting results.

The theory h-o-real-arithmetic is equipped with routines for simplifying arithmetic expressions and rational linear inequalities. These routines allow the system to perform a great deal of low-level reasoning without user intervention. The theory contains several defined entities; e.g., the natural numbers are a defined sort and the higher-order operators $\Sigma$ and $\Pi$ are defined recursively.

h-o-real-arithmetic is a useful building block for more specific theories. If a theory has h-o-real-arithmetic as a subtheory, the theory can be developed with the help of a large portion of basic, everyday mathematics. For example, in a theory of graphs which includes h-o-real-arithmetic, one could introduce the concept of a weighted graph in which nodes or edges are assigned real numbers. We imagine that h-o-real-arithmetic will be a subtheory of most theories formulated in IMPS.

   
§ sequences

Sequences over a sort $\alpha$ are represented as partial functions from the natural numbers to $\alpha$. Lists are identified with sequences whose domain is a finite initial segment of the natural numbers. The basic operations on sequences and lists, including nil, car, cdr, cons, and append are formalized as quasi-constructors.