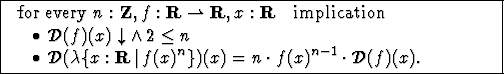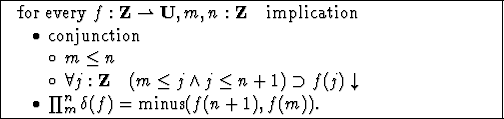


Next: 6. Little Theories
Up: 1. Introductory Material
Previous: 4. On-Line Help
Subsections
5. Exercises
This chapter describes about a dozen self-guided, content-based
exercises to illustrate the use of IMPS. Each exercise uses a
fairly self-contained piece of mathematics, logic, or computer science
to show how to organize and develop a theory in IMPS, and how to
carry out the proofs needed for the process. We will try to describe
in each case the main content of the exercise, as well as the specific
techniques that it is intended to illustrate.
We assume in this chapter that you are using the Lucid 19 menu system.
In order to start an exercise, press down
any mouse button while pointing to the IMPS-Help menubar item. Release the
button while pointing to the entry Exercises. IMPS will present a
pop-up menu listing the file names of the available exercises. Clicking on a
file name will cause the following actions:
- The system will create a new copy of the file under your own
directory, in the subdirectory
 /imps/theories. Since
this is a new file, you can safely edit it or delete it. If a file of
the expected name already exists, IMPS will prompt whether to
overwrite the file, thus destroying the previous copy.
/imps/theories. Since
this is a new file, you can safely edit it or delete it. If a file of
the expected name already exists, IMPS will prompt whether to
overwrite the file, thus destroying the previous copy.
- IMPS will create a new Emacs buffer displaying the copy.
You will use this buffer to view and edit the file.
- IMPS will search for the first item in the file meriting
your attention. Each such item will be marked by the string
(!). These items may be candidate theorems to prove, theory
declarations or definitions to read, or macetes or scripts to create.
- Anything above the first
(!) will be sent as input to
the underlying T process. Thus, IMPS will define any notions
mentioned at the top of the file.
At any point in the exercise, to proceed to the next item of interest,
select--from the IMPS-Help menubar item--the Current Exercise: Next
Entry request.
- IMPS will search for the next item in the file marked by the string
(!).
- Anything beyond the first
(!), up to the current occurrence,
will be sent as input to the underlying T process. Thus, IMPS
will install the definitions, theorems, and so forth described in that
portion of the file.
If you want to restart an exercise in a clean way, click on Exit IMPS under
General, and then on Run IMPS. The system will prompt you to confirm
the desired amount of virtual memory; the default is plenty for current
purposes. Having started a fresh invocation of IMPS, put your cursor in the
buffer that you want to work on. Click on the item Restart Exercise in
Current Buffer under IMPS-Help.
The exercises divide roughly into
four tiers of difficulty, which are summarized in Table 5.1. We
recommend that you do one or more exercises in a tier before moving on to those
in the next tier.
Table 5.1:
Exercise Files by ``Tier''
| Tier |
Exercise file name |
Section |
| 1. |
primes-exercise.t |
5.2.1 |
| |
calculus-exercise.t |
5.2.2 |
| 2. |
indicators-exercise.t |
5.3.1 |
| |
monoid-exercise.t |
5.2.3 |
| 3. |
compiler.t |
5.4.1 |
| |
limits.t |
5.2.4 |
| |
contraction.t |
5.2.5 |
| |
groups-exercise.t |
5.2.6 |
| 4. |
flatten.t |
5.4.2 |
| |
temporal.t |
5.3.2 |
|
One of the main goals of the IMPS system is to support the rigorous
development of mathematics. We hope that it will come to serve as a
mathematical data base, storing mathematical concepts, theories,
theorems, and proof techniques in a form that makes them available
when they are relevant to new work. We believe that as a consequence
IMPS will develop into a system that can serve students as a
general mathematics laboratory. In addition, we hope it will
eventually serve as a useful adjunct in mathematics research.
5.2.1 Primes
This exercise introduces two main definitions into the
theory of real arithmetic, namely divisibility and primality. It then
includes a few lemmas, which lead to a ``computational'' macete
5.1
to determine whether a positive integer is prime. After introducing the notion
of twin primes, the exercise develops two proof scripts that can be used to
find a twin prime pair in a given interval, if one exists.
A more extensive treatment of primes, including the material of this
exercise, is included in the IMPS theory library in the file
$IMPS/theories/reals/primes.t.
That file also contains statements and proofs of the following:
- the infinity of primes;
- the main properties of gcd;
- the existence and uniqueness of prime factorizations (the Fundamental
Theorem of Arithmetic).
This exercise illustrates basic definitions, and it
illustrates how to carry out several simple proofs. Its main interest however
is to illustrate the mix of computation and proof in IMPS. This balance is
reflected in the macete mechanism, and in the script that searches for a pair
of twin primes.
5.2.2 A Very Little Theory of Differentiation
This file develops a little axiomatic theory of the
derivative operator on real functions. Its axioms include the rules for:
- sum;
- product;
- constant functions;
- the identity function;
as well as the principle that the derivative of f is defined at a value xonly if f is. Naturally, these properties hold true of the derivative as
explicitly defined in the usual way.
The exercise then develops a succession of consequences of these properties,
such as the power rule shown in Figure 5.1.
Figure 5.1:
Generalized Power Rule
|
|
The properties and their consequences are then grouped together into a
macete that allows expressions involving derivatives to be
evaluated.
This exercise is intended to illustrate, in addition to
inductive reasoning, the manipulation of higher-order objects (functions
represented using 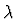 ), and the power of macetes to encode symbolic
computations.
), and the power of macetes to encode symbolic
computations.
5.2.3 Monoids
This exercises introduces a theory of monoids, a monoid
being a domain U equipped with an associative operator 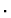 and an
identity element e. A recursive definition introduces an iterated monoid
product operator
and an
identity element e. A recursive definition introduces an iterated monoid
product operator 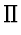 ,
such that, when
,
such that, when
 and
and
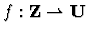 ,
then
,
then
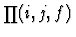 satisfies:
satisfies:
By adding an inverse operator and axioms on it, the monoid theory is extended
to a theory of groups (defined independently of the theory in
Exercise 5.2.6). The file then defines (slightly incongruously)
minus to mean:
and 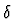 to mean:
to mean:
That is, if f is a function of sort
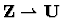 ,
then
,
then
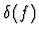 is another function of the same sort, and its value for an integer
j is the difference (in the sense of ``minus'') between f(j+1) and f(j).
is another function of the same sort, and its value for an integer
j is the difference (in the sense of ``minus'') between f(j+1) and f(j).
We can then prove the telescoping product formula shown in
Figure 5.2.
Figure 5.2:
Telescoping Product Formula
|
|
This in turn can serve as the basis of an alternative proof for
formulas such as the ones for the sum of the first n natural numbers
or of their squares. To do so, we introduce an interpretation mapping
U to R and the monoid operator 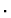 to real
addition. As a consequence, the operator
to real
addition. As a consequence, the operator 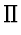 within the monoid is
carried to the (real-valued) finite summation operator
within the monoid is
carried to the (real-valued) finite summation operator 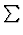 .
.
This exercise illustrates how to develop little theories
and how to apply them via interpretation. It also illustrates a simple
recursive definition.
5.2.4 Some Theorems on Limits
This exercise defines the limit of a sequence of real
numbers. A sequence of reals is represented in IMPS as a partial
function mapping integers to real numbers. The limit is defined using
the iota constructor 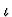 ,
where
,
where
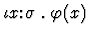 has as its value the unique value of x such that
has as its value the unique value of x such that
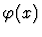 holds true. The iota-expression is undefined if
holds true. The iota-expression is undefined if 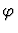 is satisfied by more
than one value or if it is not satisfied for any value. In this
case, the instance of
is satisfied by more
than one value or if it is not satisfied for any value. In this
case, the instance of 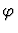 is the familiar property that, for every
positive real
is the familiar property that, for every
positive real 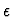 ,
there is an integer n, such that for
indices p greater than n,
,
there is an integer n, such that for
indices p greater than n,
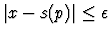 .
.
Theorems include a variant of the definition in which iota
does not occur, as well as the familiar condition for the existence of
the limit. The homogeneity of limit is also proved.
The main purpose of this exercise is to illustrate how to
reason with iota. In particular, it illustrates the
importance of deriving an ``iota-free'' characterization for a notion
defined in terms of iota.
5.2.5 Banach's Fixed Point Theorem
This extensive file, contraction.t, contains a
complete proof of Banach's contractive mapping fixed point theorem.
An alternative proof using a little more general machinery is
contained in the theory library in file
$IMPS/theories/metric-spaces/fixed-point-theorem.t
The theorem states that in a complete metric space
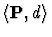 ,
any contractive function has a unique fixed point. A function f is
contractive if, there exists a real value k<1 such that for all points xand y in P,
,
any contractive function has a unique fixed point. A function f is
contractive if, there exists a real value k<1 such that for all points xand y in P,
The heart of the proof is to show that under this condition the sequence sof iterates of f starting from an arbitrary point x,
will converge. It is then easy to show that the limit of s is a fixed point.
Finally, if any two distinct points x and y were both fixed, then we would
have
This theorem serves as a very good illustration of IMPS's ``little
theories'' approach. It combines:
- Concrete theorems about the reals, such as the geometric series
formula, which are needed to bound the differences between points in
s;
- A few abstract facts about the sequence of iterates of a function,
which are perfectly generic and independent of the fact that we will
eventually apply them to functions
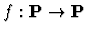 ;
;
- A third group of theorems proved in the theory of a metric space,
applying the previous theorems.
The exercise has three purposes:
- To illustrate the little theories approach and how natural it is in
mathematics;
- To illustrate inductive proof (in combination with some other
techniques) in real arithmetic and also in the generic theory covering
iteration;
- To provide a richer, more extended example of how to develop a
substantial proof using IMPS.
5.2.6 Basics of Group Theory
This file develops the very rudiments of group theory,
only up to a definition of subgroup and a proof that subgroups are
groups. Most of the content is devoted to building up computational
lemmas. This exercise covers only a very small part of the portion of
group theory that is developed in the IMPS theory library, in
the files contained in the directory:
$IMPS/theories/groups/
The purpose of this exercise is to illustrate how to
handcraft the simplification mechanism by proving rewrite rules. In addition,
a compound macete is introduced to carry out computations not suited to the
simplifier. The file also illustrates the use of a symmetry translation
mapping the theory to itself. This translation maps the multiplication
operator 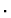 to
to
Thus, for instance, right
cancellation follows by symmetry from left cancellation.
5.3.1 Indicators: A Representation of Sets
An indicator is a function used to represent a set. It has a sort of
the form
![$[\alpha, \mbox{unit\%sort}]$](img59.gif) ,
where
,
where 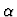 is an arbitrary
sort. (In the string syntax, the sort
is an arbitrary
sort. (In the string syntax, the sort
![$[\alpha, \mbox{unit\%sort}]$](img59.gif) is printed as sets[
is printed as sets[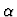 ].) unit%sort is a
type in the-kernel-theory that contains exactly one element
named an%individual. The type is of kind
].) unit%sort is a
type in the-kernel-theory that contains exactly one element
named an%individual. The type is of kind 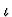 ,
so
indicators may be partial functions. Since the-kernel-theory is a component theory of every IMPS theory,
unit%sort is available in every theory.
,
so
indicators may be partial functions. Since the-kernel-theory is a component theory of every IMPS theory,
unit%sort is available in every theory.
Indicators are convenient for representing sets. The basic idea is
that a set s containing objects of sort 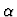 can be represented
by an indicator of sort
can be represented
by an indicator of sort
![$[\alpha, \mbox{unit\%sort}]$](img59.gif) ,
namely the one
whose domain is s itself. Simplifying expressions involving
indicators is to a large extent a matter of checking definedness--for
which the simplifier is equipped with special-purpose algorithms. The
theory indicators consists of just a single base sort U, for the ``universe'' of some unspecified domain. Since the theory
indicators contains no constants nor axioms, theory
interpretations of indicators are trivial to construct, and
thus theorems of indicators are easy to use as transportable
macetes.
,
namely the one
whose domain is s itself. Simplifying expressions involving
indicators is to a large extent a matter of checking definedness--for
which the simplifier is equipped with special-purpose algorithms. The
theory indicators consists of just a single base sort U, for the ``universe'' of some unspecified domain. Since the theory
indicators contains no constants nor axioms, theory
interpretations of indicators are trivial to construct, and
thus theorems of indicators are easy to use as transportable
macetes.
The logical operators in IMPS are fixed, but quasi-constructors can in some respects effectively serve as
additional logical operators. Quasi-constructors are desirable for
several reasons:
- Once a quasi-constructor is defined, it is available in every theory
whose language contains the quasi-constructor's home language. That
is, a quasi-constructor is a kind of global constant that can
be freely used across a large class of theories. (A constructor, which
we also call a logical constant, is available in every theory.)
- Quasi-constructors are polymorphic in the sense that they can
be applied to expressions of several different types. (Several of the
constructors, such as = and if, are also polymorphic in
this sense.)
- Quasi-constructors are preserved under translation. Hence, to reason
about expressions involving a quasi-constructor, we may prove laws
involving the quasi-constructor in a single generic theory. The
translation mechanism can then be used to apply the theorems to
expressions in any theory that involve the same quasi-constructor.
- Quasi-constructors can be used to represent operators in nonclassical
logics, such as modal or temporal logics (see
Section 5.3.2), and operators on generic objects such as
sets (as represented by indicators) and sequences.
Quasi-constructors are implemented as ``macro/abbreviations.'' The IMPS
reader treats them as macros which cause the creation of a particular syntactic
pattern in the expression, while the IMPS printer is responsible for
printing them in abbreviated form (wherever those patterns may have arisen).
The exercise derives a few facts about sets, their unions, and the inclusion
relation. It applies them to intervals of integers.
The purpose of this exercise is to provide experience
reasoning with quasi-constructors.
5.3.2 Temporal Logic
Temporal logic is a kind of modal logic for reasoning about dynamic
phenomenon. In recent years temporal logic has won favor as a logic
for reasoning about programs, particularly concurrent programs. The
following is an exercise to develop a version of propositional
temporal logic ( PTL) in IMPS.
In this exercise we view time as discrete and linear; that is, we identify time
with the integers. The goal of the exercise is to build machinery for
reasoning about ``time predicates,'' which are simply expressions of sort
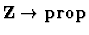 .
In traditional PTL, the time argument
is suppressed and objects which are syntactically formulas are manipulated
instead of syntactic predicates. In IMPS we will deal directly with the
predicates.
.
In traditional PTL, the time argument
is suppressed and objects which are syntactically formulas are manipulated
instead of syntactic predicates. In IMPS we will deal directly with the
predicates.
This is a very open-ended exercise, which should be done after the user is
fairly familiar with IMPS and its modus operandi.
IMPS also provides some facilities for reasoning about computing
applications, although these are still less extensive than those for
mathematics. The exercises illustrate a facility for defining recursive data
types, as well as an application of a theory of state machines.
5.4.1 The World's Smallest Compiler
This exercise introduces two syntaxes as
abstract data types. Each syntax is given a semantics as a simple
programming language. A function defined by primitive recursion on
one language (the ``source language'') maps its expressions to values
in the other (the ``target language''). This function is the
compiler. We prove that the semantics of its output code matches the
semantics of its input.
The primary purpose of this exercise is to illustrate the
BNF mechanism for introducing a recursive abstract data type. Connected
with a BNF is a schema for recursion on the data type. This is a form of
primitive recursion, as distinguished from IMPS's more general facility for
monotone inductive definitions. The primitive recursion schema is preferable
when it applies because it automatically creates rewrite rules for the separate
syntactic cases.
A secondary purpose is to illustrate in a very simple case an approach to
compiler verification.
5.4.2 A Linearization Algorithm for a Compiler
A linearizer is a compiler component responsible for
transforming a tree-like intermediate code into a linear structure. Its
purpose is typically to transform (potentially nested) conditional statements
into the representation using branch and conditional branch instructions that
take numerical arguments. The exercise is contained in the file
flatten.t.
It also depends on the BNF and primitive recursion mechanisms. However,
the proofs have more interesting induction hypotheses than in the world's
smallest compiler, and the development calls for an auxiliary notion of
``regular'' instruction sequences.
This exercise can be used as a more realistic and
open-ended example of a computer science verification.
This exercise consists of two files, namely:
- $IMPS/theories/exercises/fun-thm-security.t
- $IMPS/theories/exercises/bell-lapadula.t
The first file proves the Bell-LaPadula ``Fundamental Theorem of Security'' in
the context of the theory of an arbitrary deterministic state machine with a
start state, augmented by an unspecified notion of ``secure state.'' (A
similar theorem also holds for nondeterministic state machines.) The proof is
by induction on the accessible states of the machine.
The second file instantiates this theory in the case of a simple access control
device (reference monitor). The states are functions, which, given a subject
and an object returns a pair; one component of the pair represents whether the
subject has current read access to the object, while the other represents
current write access. The operations of the machine correspond to four
requests by a subject concerning an object; the request may be to add or delete
and access, which may in turn be either read or write access. The subjects and
objects have security levels, and the requests are adjudicated based on their
levels.
The theory exploits the fact that read and write are duals, when the sense of
the partial ordering on levels is inverted. This duality is expressed by means
of a theory interpretation mapping the theory to itself. It is used to
manufacture definitions; for instance, the *-property is defined to be
the dual of the simple security property. It is also used to create new
theorems. For instance, the theorem that the *-property is preserved under
get-write is the dual of the theorem that the simple security property is
preserved under get-read; hence, it suffices to prove the latter, and the
former follows automatically.
This exercise has three main purposes:
- To illustrate how to extend and to apply the state machine theory, and
how to prove theorems using state machine induction;
- To illustrate the use of an interpretation from a theory to itself to
encode a ``symmetry'' or ``duality;''
- To provide a model for a familiar kind of security verification.



Next: 6. Little Theories
Up: 1. Introductory Material
Previous: 4. On-Line Help
System Administrator
2000-07-23