


Next: 13. Simplification
Up: 2. User's Guide
Previous: 11. Theory Ensembles
Subsections
12. The Proof System
In purpose of this chapter is to explain:
- The IMPS proof system.
- A description of how you prove theorems in IMPS, in interactive mode and
in script mode.
- A description of the proof-script language.
A proof of a statement  is conclusive mathematical
evidence of why
is conclusive mathematical
evidence of why  is true. A proof is usually thought of as a
sequence of formulas
is true. A proof is usually thought of as a
sequence of formulas
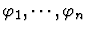 such that
such that
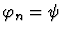 and every
and every 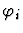 is either:
is either:
- 1.
- An axiom, that is, a formula which is assumed true to begin with;
- 2.
- A theorem, that is, a formula whose truth has already been
established by some other proof; or
- 3.
- A consequence of one or more previous formulas in the sequence.
This means that
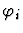 is related to these formulas by a relation
called an inference.
is related to these formulas by a relation
called an inference.
The criterion for determining what constitutes an acceptable inference
depends on the purpose of the proof. If the proof is for mechanical
verification only (whether by a digital computer or a human being
acting like one), then the criteria of acceptability can be specified
unambiguously as a set of rules for determining which sequences of
symbols constitute proofs. This set of rules is called a proof
system. For a human audience, on the other hand, it is usually a good
idea to stress the essential or innovative steps in a proof and avoid
routine computations. Moreover, for an expository article, a textbook,
or a classroom lecture, it is acceptable, even desirable, that
inference steps appeal to intuition.
In the traditional presentation of proofs in textbooks and journals,
the deductive process appears as an inexorable progression from known
facts to unknown ones. In contrast, the deductive process in IMPS begins with a conjecture and usually proceeds with a large amount of
trial and error. This view of the deductive process leads naturally
to the idea of a proof as a graph.
Proofs in IMPS are represented by a data structure called a deduction graph, which is a directed graph with two kinds of nodes:
inference nodes and sequent nodes. A sequent node consists
of a single formula called the assertion together with a context. The context is logically a set of assumptions, although the
implementation caches various kinds of derived information with a
context. An inference node i consists of a unique conclusion
node c, a (possibly empty) set of hypothesis nodes
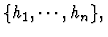 and the mathematical justification for asserting the
relationship between c and
and the mathematical justification for asserting the
relationship between c and
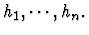 This justification is
called an inference rule.
This justification is
called an inference rule.
As an interactive process, a proof consists of a series of
reductions of unproven sequent nodes of the graph (which we think of as
goals) to new subgoals. Each reduction is created by a
procedure called a primitive inference procedure, which takes
a sequent node and possibly other arguments, returns an inference node
inf and, as a side-effect, changes the deduction graph. These changes
include:
- The addition of inf to the set of inference nodes of
the deduction graph.
- The addition of the hypotheses of inf to the set of sequent nodes.
There are about 25 primitive inference procedures. Primitive
inference procedures are the only means by which inference nodes can
be added to a deduction graph. As a user of IMPS, however, you will
never apply primitive inference procedures directly; you will only
apply them indirectly by applying proof commands--convenient
procedures which add sequent nodes and inference nodes to a deduction
graph by calling primitive inferences. Proof commands are documented
in Chapter 18.
12.3 Theorem Proving
There are two modes of proving theorems in IMPS: interactive
mode and script mode. Interactive mode is used for proof
discovery and interactive experimentation with new proof techniques.
Script mode is used primarily for proving theorems whose proofs are
similar to previously constructed proofs or for checking a large
number of proofs.
To begin an interactive proof, select the Start dg option in
the menu or use the Emacs command M-x imps-start-deduction.
IMPS will then prompt you in the minibuffer with the text Formula or reference number: which you can supply by clicking the
right mouse button on the formula you want to prove (provided it
is enclosed between double quotes) or by typing the reference number
of the formula (provided it has already been built). All the proof commands
and node-movement commands given during the course of a single proof
are recorded as a component of the deduction graph. These commands
can be inserted as text into a buffer (provided the major mode of the
buffer is scheme mode) by selecting the option Insert proof
script or by entering C-c i. The text that is inserted in
the buffer is a script of proof commands which can be edited and used
in other proofs. To run a command script, select the option Execute region or enter C-c r. This will run the commands
in the current region. Note that an interactive proof can be combined
with one or more proof segments run in script mode. This is especially
useful for redoing similar arguments.
12.3.1 Checking Proofs in Batch
To check a large number of proofs, (for example, to check an addition to the
theory library) proof scripts can be run in batch by
using the shell command
$IMPS/../bin/run_test testfile logfile
where testfile is a text file which may contain any def-form. Typically, it will consist of a series of include-files and load-section forms. The file logfile
will contain the output of the process.
For example, entering on a machine called veraguas the shell command
$IMPS/../bin/run_test testy loggy
where testy contains
(load-section abstract-calculus)
will produce a logfile loggy which will look something like:
HOST veraguas starting IMPS test.
File tested = testy
Executable = /imps/sys/executables/foundation
Mon May 3 18:21:56 EDT 1993
INITIAL THEORY NETWORK INFORMATION:
THEORIES = 12
THEORY-INTERPRETATIONS = 1
THEOREMS = 277
MACETES = 360
EXPRESSIONS = 3428
1. THEOREM-NAME: ANONYMOUS
forall(a,c:uu,
forsome(b:uu,b prec a and c prec b) implies c prec a);
THEORY: PARTIAL-ORDER
SEQUENT NODES: 10
PROOF STEPS: 3
GROUNDED?: YES
CONTEXTS=4
ASSUMPTIONS/CONTEXT=1.0
virtual time = 0.16 seconds
.
.
.
219. THEOREM-NAME: LOCALITY-OF-INTEGRALS
forall(phi,psi:[ii,uu],a,b:ii,
a<b
and
integrable(phi)
and
integrable(psi)
and
forall(x:ii,a<=x and x<b implies phi(x)=psi(x))
implies
forall(x:ii,
a<=x and x<b implies
integral(a,x,phi)=integral(a,x,psi)));
THEORY: MAPPINGS-FROM-AN-INTERVAL-TO-A-NORMED-SPACE
SEQUENT NODES: 54
PROOF STEPS: 33
GROUNDED?: YES
CONTEXTS=29
ASSUMPTIONS/CONTEXT=5.551724137931035
virtual time = 25.05 seconds
0 errors during test.
0 failed proofs during test.
FINAL THEORY NETWORK INFORMATION:
THEORIES = 32
THEORY-INTERPRETATIONS = 110
THEOREMS = 915
MACETES = 1108
EXPRESSIONS = 89274
Mon May 3 21:06:38 EDT 1993
IMPS test completed.
Informally, a script is a sequence of proof commands and control
statements. Essentially, the script facility in IMPS allows users to
build programs to prove theorems. Scripts are a useful way to package
and reuse common patterns of reasoning. The paper [8]
presents some practical methods for exploiting the IMPS proof script
mechanism.
A script is a kind of s-expression, that is, a symbol, a string, an
integer, or a nested-list of such objects. To describe how IMPS interprets scripts to modify the state of the deduction graph, we
first establish some terminology to designate certain classes of
script components. Each script component is itself an s-expression.
- A script form expression (expression for short) is a string, a
symbol, a number, or a list of expressions.
- An expression operator is one of the symbols
%, *, ~*.
- A script variable is a symbol beginning with $.
- A keyword form is a list whose first element is one
of the following symbols (which we refer to as keywords): move-to-sibling,
move-to-ancestor, move-to-descendent, block, if, for-nodes, while, let-script, let-macete,
let-val, script-comment, label-node, jump-to-node, skip.
- A command form is an expression which is either a command name
or a list whose first element is a command name.
- A script is a list of script form expressions.
In Figure 12.1 we provide an example of a script. This
script can be used to prove the combinatorial identity discussed in
Chapter ![[*]](cross_ref_motif.gif) on the IMPS micro exercises. The script
consists of a number of forms, each of which is applied to a unique node of
the deduction graph called the current node. In interactive mode,
the current node is the one which is displayed in the sequent node buffer.
on the IMPS micro exercises. The script
consists of a number of forms, each of which is applied to a unique node of
the deduction graph called the current node. In interactive mode,
the current node is the one which is displayed in the sequent node buffer.
Figure 12.1:
An IMPS Proof Script
 |
- 1.
- Expand the definition of comb, which in IMPS is
given in terms of the factorial function. The resulting sequent
consists of a context containing the formulas
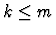 and
and 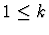 and the assertion
and the assertion
- 2.
- Apply the macete fractional-expression-manipulation to the
sequent above. Moreover, attach to the label compound, to the
resulting node, but otherwise leave the deduction graph intact. This
will allow us to subsequently return to this node.
- 3.
- Apply the command direct-and-antecedent-inference-strategy to
the result of the previous step. This adds three new sequents to the
deduction graphs: two concerning definedness and one whose assertion
is an equation.
- 4.
- We will process these nodes in step by iterating
through them with the (for-nodes) keyword form as follows:
- (a)
- For the sequents concerning definedness,
use the macete definedness-manipulations. This combines a number of
facts about the definedness of the arithmetic operations and the
factorial function.
- (b)
- For the remaining sequent, use the macete
factorial-reduction.
Scripts are executed in an environment. This environment is an
association of symbols to values. Every script expression has a value
in the script's execution environment. The value of a script
expression is determined as follows:
- If the expression is a script variable $n where n is an integer,
then the value is the n-th argument in the script call.
- If the expression is a script variable $name where name is a symbol,
its value is determined by the last assignment of that variable. If
there is no assignment preceding the call, an error is raised.
- If the expression is a string, an integer, or a symbol which
is not a variable, then the value of the expression is itself.
- If the expression is a list whose first element is an expression operator,
(that is, one of the symbols
%, *, ~*) then that
operator is applied to the values of the arguments as follows:
(%
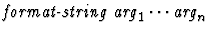 ).
The first argument must be a string with exactly n occurrences
of the characters
).
The first argument must be a string with exactly n occurrences
of the characters ~A. The remaining arguments
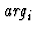 are plugged in
succession for each occurrence of
are plugged in
succession for each occurrence of ~A.
(%sym
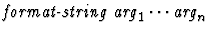 ).
The first argument must be a string with exactly n occurrences of
the characters
).
The first argument must be a string with exactly n occurrences of
the characters ~A. The remaining arguments
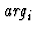 are plugged in succession for each occurrence of
are plugged in succession for each occurrence of ~A and the
resulting string is read in as a symbol.
(*
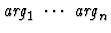 ).
The set of assumptions (regarded as strings) of the current sequent
node which match any argument.
).
The set of assumptions (regarded as strings) of the current sequent
node which match any argument.
(~*
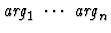 ).
The set of assumptions (regarded as strings) of the current sequent
node which match no argument.
).
The set of assumptions (regarded as strings) of the current sequent
node which match no argument.
- If the expression is a list whose first element is not an
expression operator, its value is the list of values of the arguments.
A script is a list
(
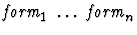 of script expressions. The interpreter executes
each form in the script in left-to-right order12.1. Once a form is executed by the script interpreter at a
sequent node S, execution of the script continues at a new sequent
node S1 called the natural continuation node of the script.
This node is usually the first ungrounded relative of S after the form is executed. The only exception is when the form is a
node motion keyword form.
of script expressions. The interpreter executes
each form in the script in left-to-right order12.1. Once a form is executed by the script interpreter at a
sequent node S, execution of the script continues at a new sequent
node S1 called the natural continuation node of the script.
This node is usually the first ungrounded relative of S after the form is executed. The only exception is when the form is a
node motion keyword form.
The rules for script interpreter execution are given below.
Interpreting a script expression
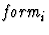 usually causes
side effects on the current deduction graph and other structures
associated to the current proof. The side-effects depend on the kind
of form being handled by the interpreter.
usually causes
side effects on the current deduction graph and other structures
associated to the current proof. The side-effects depend on the kind
of form being handled by the interpreter.
Recall that a keyword form is a script expression which is a list
whose first element is a keyword. The execution of keyword forms
depends on the keyword:
- Node motion forms. These forms cause script execution to continue
at a node other than the natural continuation node. The following are the node motion
keyword forms:
- (move-to-sibling n). This causes execution to
proceed at the n-th sibling node.
- (move-to-ancestor n). This causes execution to
proceed at the n-th ancestor node.
- (move-to-descendent (
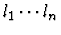 )).
This causes execution to proceed at the specified descendent node.
Each li is an integer or a dotted pair
)).
This causes execution to proceed at the specified descendent node.
Each li is an integer or a dotted pair
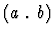 of integers.
of integers.
- (jump-to-node label). label is a deduction graph
sequent node label.
- Conditionals. (if test-form consequent alternative)
These are forms which provide conditional
execution of command forms. The test-form
can be of the following kinds:
- Blocks.
(block
 ). A block form merely provides a grouping for a
list of script forms.
). A block form merely provides a grouping for a
list of script forms.
- Iteration forms. These are of two kinds:
- Range iterations provide for execution over a specified range of nodes.
These have the form (for-nodes range-form script-form).
range-form can be one of the following:
- (unsupported-descendents).
- (minor-premises).
- (node-and-siblings).
- Conditional iterations provide for execution while a specified condition holds.
These have the form (while test-form script-form), where
test-form is specified in the same way as for conditional forms.
- Skip. (skip). This is a form used to insert in locations where at least
one script form is required. It is essentially equivalent to (block).
- Assignments.
- (let-script name arg-count script). This form adds a command
with name $name. The value of $name is this name in the current
execution environment.
- (let-macete name compound-macete-specification). This form adds a macete with name $name. The value of $name is this name in the current
execution environment.
- (let-val name expression). The value of $name is this name
in the current execution environment.
- Deduction graph node labels.
- (label-node name). This form assigns the label
name to the current node.
All these forms modify the current execution environment.
- Comments. (script-comment comment-string). Adds a comment to the preceding
history entry. This keyword form has no other effect.
Execution of any other form form
in a script has the following result: The value of form must be
a command form which is applied to the current node. In other words:
- If the value of form is a symbol, this
value should be the name of a command which takes no arguments;
otherwise an error results. The script interpreter then applies that
command to the current sequent node.
- If the value of form is a list, the first expression of the list must
be the name of a command, while the remaining elements should be
arguments of the command; otherwise an error results. The script
interpreter then applies that command with the resulting arguments to
the current sequent node.
The following are possible arguments to a command:
- A symbol. Depending on the command and the location of the argument, this symbol
may refer to a theorem, a macete, a translation, an inductor,
a quasi-constructor, or a constant.
- A string. This string can be used to refer to an expression,
a theorem, or a context.
- An integer. This integer can be used to refer to a sequent node, an occurrence number
within an expression, or the number of an assumption.
- A list of strings.
- A list of integers.
- 1.
- To build a proof script for insertion in a def-theorem form, it is
much easier to first prove the theorem interactively and then record the proof
script using C-c i. A novice user should not attempt to build scripts from
scratch without thoroughly understanding how scripts replay interactive proofs.
- 2.
- More experienced users can build new scripts by modifying
existing ones. For example, the following is a def-theorem form
with a valid proof:
(def-theorem MIN-LEMMA
"forall(a,b,c:rr,
a<b and a<c
implies
forsome(d:rr, a<d and d<=b and d<=c))"
(theory h-o-real-arithmetic)
(proof
(
direct-and-antecedent-inference-strategy
(instantiate-existential ("min(b,c)"))
(unfold-single-defined-constant-globally min)
(case-split ("b<=c"))
simplify
simplify
(apply-macete-with-minor-premises minimum-1st-arg)
(apply-macete-with-minor-premises minimum-2nd-arg)
)))
To get a valid proof for an analogous theorem where the arguments to < and  are
interchanged, one can edit the previous script replacing min by max
everywhere in the proof:
are
interchanged, one can edit the previous script replacing min by max
everywhere in the proof:
(def-theorem MAX-LEMMA
"forall(a,b,c:rr,
b<a and c<a
implies
forsome(d:rr, d<a and b<=d and c<=d))"
(theory h-o-real-arithmetic)
(proof
(
direct-and-antecedent-inference-strategy
(instantiate-existential ("max(b,c)"))
(unfold-single-defined-constant-globally max)
(case-split ("b<=c"))
simplify
simplify
(apply-macete-with-minor-premises maximum-1st-arg)
(apply-macete-with-minor-premises maximum-2nd-arg)
)))



Next: 13. Simplification
Up: 2. User's Guide
Previous: 11. Theory Ensembles
System Administrator
2000-07-23
![]() is conclusive mathematical
evidence of why
is conclusive mathematical
evidence of why ![]() is true. A proof is usually thought of as a
sequence of formulas
is true. A proof is usually thought of as a
sequence of formulas
![]() such that
such that
![]() and every
and every ![]() is either:
is either:
![]() and the mathematical justification for asserting the
relationship between c and
and the mathematical justification for asserting the
relationship between c and
![]() This justification is
called an inference rule.
This justification is
called an inference rule.
![[*]](cross_ref_motif.gif) on the IMPS micro exercises. The script
consists of a number of forms, each of which is applied to a unique node of
the deduction graph called the current node. In interactive mode,
the current node is the one which is displayed in the sequent node buffer.
on the IMPS micro exercises. The script
consists of a number of forms, each of which is applied to a unique node of
the deduction graph called the current node. In interactive mode,
the current node is the one which is displayed in the sequent node buffer.
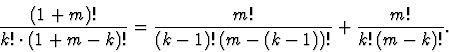
![]() of script expressions. The interpreter executes
each form in the script in left-to-right order12.1. Once a form is executed by the script interpreter at a
sequent node S, execution of the script continues at a new sequent
node S1 called the natural continuation node of the script.
This node is usually the first ungrounded relative of S after the form is executed. The only exception is when the form is a
node motion keyword form.
of script expressions. The interpreter executes
each form in the script in left-to-right order12.1. Once a form is executed by the script interpreter at a
sequent node S, execution of the script continues at a new sequent
node S1 called the natural continuation node of the script.
This node is usually the first ungrounded relative of S after the form is executed. The only exception is when the form is a
node motion keyword form.
![]() usually causes
side effects on the current deduction graph and other structures
associated to the current proof. The side-effects depend on the kind
of form being handled by the interpreter.
usually causes
side effects on the current deduction graph and other structures
associated to the current proof. The side-effects depend on the kind
of form being handled by the interpreter.