


Next: 16. Syntax: Parsing and
Up: 2. User's Guide
Previous: 14. Macetes
Subsections
The iota or 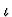 constructor is a definite description
operator for objects of kind
constructor is a definite description
operator for objects of kind 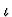 .
Given a variable x of sort
.
Given a variable x of sort
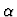 of kind
of kind 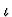 and a unary predicate
and a unary predicate 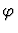 ,
,
denotes the unique x that
satisfies 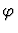 if there is such an x and is undefined
otherwise. For example,
if there is such an x and is undefined
otherwise. For example,
denotes 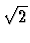 but
but
is
undefined.
The iota constructor is very useful for specifying
functions, especially partial functions. For example, ordinary
division of sort
![$[{\bf R},{\bf R},{\bf R}]$](img408.gif) (which is undefined
whenever its second argument is 0) can be defined from the times
function
(which is undefined
whenever its second argument is 0) can be defined from the times
function  by the lambda-expression
by the lambda-expression
Of course, this kind of definite
description operator is only possible in a logic that admits undefined
expressions.
An iota-expression is any expression which begins with the
iota constructor (without any abbreviations by
quasi-constructors). Proving a sequent with an assertion containing
an iota-expression can be tricky. The key idea is to reduce the
sequent to a new sequent with one less iota-expression. This is
called ``eliminating iota.'' There are two commands and one macete for
eliminating iota, each of which is discussed below in a separate
subsection.
This command, which is described in Chapter 18, is the
best iota-elimination tool in IMPS. Generally, you should use it
whenever you want to eliminate an iota-expression whose definedness is
implied by the sequent's context. It can also be used effectively in
some cases on an iota-expression E whose definedness is not implied
by the sequent's context. This is done by applying case-split with
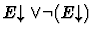 ,
followed by applying
eliminate-defined-iota-expression on the
,
followed by applying
eliminate-defined-iota-expression on the
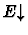 case.
case.
The eliminate-defined-iota-expression command is
multi-inference; it adds about 20 new sequent nodes to a deduction
graph.
This command is also described in Chapter 18. It is a
single-inference command that is applicable to just atomic and negated
atomic formulas. You should use it when you want to eliminate an
iota-expression whose definedness is not implied by the sequent's
context.
This is a compound macete with built-in abstraction specified by:
(def-compound-macete ELIMINATE-IOTA-MACETE
(sequential
iota-abstraction-macete
(series
tr%defined-iota-expression-elimination
tr%negated-defined-iota-expression-elimination
tr%left-iota-expression-equation-elimination
tr%right-iota-expression-equation-elimination)
beta-reduce))
The four elimination theorems are in the file $IMPS/theories/generic-theories/iota.t. You should try eliminate-iota-macete when the assertion has one of the following
forms:
- 1.
-
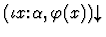
- 2.
-
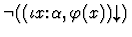
- 3.
-
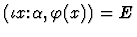
- 4.
-
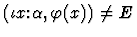
- 5.
-
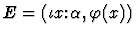
- 6.
-
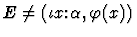
- 7.
-
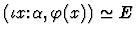
- 8.
-
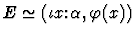
For forms (1)-(6), the macete can be applied immediately, but for
forms (7) and (8), the command insistent-direct-inference
must be applied first. Beware that, for various reasons, eliminate-iota-macete may fail to do anything, in which case you
should use one of the two iota-elimination commands.
- 1.
- Suppose E is an expression of sort
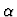 .
Sometimes it
is convenient to have a new expression E' of sort
.
Sometimes it
is convenient to have a new expression E' of sort 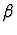 (where
(where
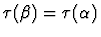 but
but
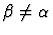 )
such that Eand E' have the same denotation. Such an expression can be easily
constructed from E and
)
such that Eand E' have the same denotation. Such an expression can be easily
constructed from E and 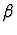 using iota:
using iota:
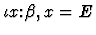 is quasi-equal to E and is of sort
is quasi-equal to E and is of sort 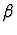 .
For
example,
.
For
example,
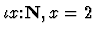 denotes the natural number
2. It is important to mention here that the IMPS simplifier
reduces an iota-expression of the form
denotes the natural number
2. It is important to mention here that the IMPS simplifier
reduces an iota-expression of the form
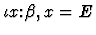 to
the conditional
to
the conditional
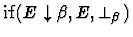 ,
and further to
E or
,
and further to
E or
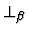 if it can decide the formula
if it can decide the formula
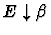 .
.
- 2.
- Suppose f is a function constant defined to be
such that
the following ``existence implies uniqueness'' theorem holds for
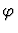 :
:
By virtue of this theorem, there is an ``iota-free characterization''
of f,
which enables one to prove a formula f(a)=b by showing
only existence--without employing any of the aforementioned tools for
eliminating iota.
As an example, consider the limit operator lim%rr on sequences of reals defined by:
(def-constant LIM%RR
"lambda(s:[zz,rr], iota(x:rr, forall(eps:rr,
0<eps
implies
forsome(n:zz, forall(p:zz,
n<=p implies abs(x-s(p))<=eps)))))"
(theory h-o-real-arithmetic))
Since a sequence always has at most one limit point, there is an
iota-free characterization of lim%rr:
(def-theorem CHARACTERIZATION-OF-REAL-LIMIT
"forall(s:[zz,rr],
x:rr,lim%rr(s)=x
iff
forall(eps:rr,
0<eps
implies
forsome(n:zz, forall(p:zz,
n<=p implies abs(x-s(p))<=eps))))"
(theory h-o-real-arithmetic))
- 3.
- It is rarely a good idea to unfold a constant defined as an
iota-expression, if it has an iota-free characterization. Instead, the
following steps are suggested. For concreteness, let us assume the
constant we are unfolding is a function constant f as in the
previous item. Our aim is to reduce all occurrences of f to
occurrences of the form f(a)=b,
- If all occurrences in the formula are of the
form f(a)=b then apply the iota-free characterization of f as a
macete.
- Otherwise, for every occurrence f(a), where a is a
free variable, cut with the formula
Each application of cut adds two new sequent nodes to
the deduction graph:
- The cut major premise, which is the original sequent plus
the cut formula as another assumption.
- The cut minor premise, which has the cut formula as the assertion.
The minor premise can be proved by instantiating y with
f(a). To proceed with this part of the proof you
will need to establish the definedness of f(a).
For a precise description of the sequent nodes added by cut, see
the documentation on the command cut-with-single-formula.
- To deal with the major premise, do an antecedent inference on the
cut formula to remove its existential quantifier. This yields a new goal
with an assumption of the form f(a)=v.
- Backchain repeatedly on f(a)=v. This replaces all occurrences of f(a) with
v.
- Incorporate the antecedent f(a)=v and apply the iota-free characterization
of f as a macete. This should replace all such occurrences with
some condition not involving f, and more importantly, not involving
iota.
- 4.
- The iota-p constructor is a definite
description operator for objects of kind
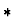 .
It has a different
semantics than iota: if there is no unique x of sort
.
It has a different
semantics than iota: if there is no unique x of sort
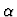 satisfying a unary predicate
satisfying a unary predicate 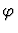 ,
then
,
then
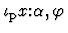 is defined (like all expressions
of kind
is defined (like all expressions
of kind 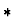 )
but has the value
)
but has the value
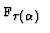 .
There is currently no support in IMPS for reasoning about the
iota-p. This should not cause you any concern because
iota-p has little practical value.
.
There is currently no support in IMPS for reasoning about the
iota-p. This should not cause you any concern because
iota-p has little practical value.



Next: 16. Syntax: Parsing and
Up: 2. User's Guide
Previous: 14. Macetes
System Administrator
2000-07-23
![]() constructor is a definite description
operator for objects of kind
constructor is a definite description
operator for objects of kind ![]() .
Given a variable x of sort
.
Given a variable x of sort
![]() of kind
of kind ![]() and a unary predicate
and a unary predicate ![]() ,
,
![]() (which is undefined
whenever its second argument is 0) can be defined from the times
function
(which is undefined
whenever its second argument is 0) can be defined from the times
function ![]() by the lambda-expression
by the lambda-expression ![]() ,
followed by applying
eliminate-defined-iota-expression on the
,
followed by applying
eliminate-defined-iota-expression on the
![]() case.
case.