


Next: 20. The Initial Theory
Up: 3. Reference Manual
Previous: 18. The Proof Commands
Subsections
19. The Primitive Inference Procedures
In this chapter we list and document each of the primitive inference
procedures. We will use the following format to describe them.
- Parameters.
- A list of the arguments (other than the sequent node)
required by procedure. These arguments can be of the following types:
- A formula.
- A list of formulas.
- A path represented as a list of nonnegative integers.
- A list of paths.
- A constant.
- A macete.
- Another sequent node (usually referred to as the major premise).
- Description.
- A brief description of the primitive inference.
Some of primitive inference procedures have descriptions which are
identical to the description of the corresponding interactive proof
command.
antecedent-inference
A sequent node assumption.
The effect of applying this primitive
inference procedure is given by the following table.
| Conclusion |
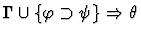 |
| Premises |
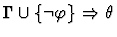 |
| |
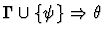 |
| Conclusion |
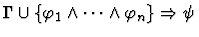 |
| Premise |
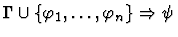 |
| Conclusion |
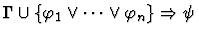 |
Premises
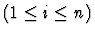 |
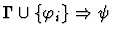 |
| Conclusion |
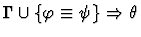 |
| Premises |
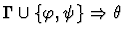 |
| |
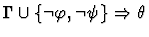 |
| Conclusion |
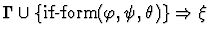 |
| Premises |
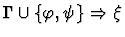 |
| |
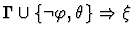 |
| Conclusion |
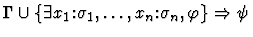 |
| Premise |
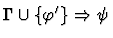 |
Notes:
- Each sequent in the preceding table is of
the form
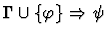 ,
where
,
where
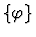 is the parameter to the primitive inference procedure.
is the parameter to the primitive inference procedure.
-
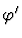 is obtained from
is obtained from 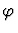 by renaming the
variables among
by renaming the
variables among
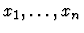 which are free in both
which are free in both 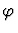 and
the original sequent.
and
the original sequent.
backchain-inference
A sequent node assumption.
This primitive inference procedure attempts to use the assumption given as argument to
replace the assertion to be proved. In the simplest case, if the
given assumption is
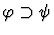 and the assertion is
and the assertion is 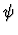 ,
then backchain-inference replaces the assertion with
,
then backchain-inference replaces the assertion with 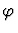 .
Similarly, if the assertion is
.
Similarly, if the assertion is
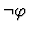 ,
it is replaced with
,
it is replaced with
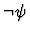 .
The command extends this simplest case in four ways:
.
The command extends this simplest case in four ways:
- If the assumption is universally quantified, then matching is used to
select a relevant instance.
- If the assumption is a disjunction
then, for any 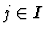 ,
it may be treated as
,
it may be treated as
- If the assumption is of one of the forms s=t,
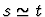 ,
,
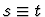 ,
if a subexpression of the assertion matches s, then
it is replaced by the corresponding instance of t.
,
if a subexpression of the assertion matches s, then
it is replaced by the corresponding instance of t.
- If the assumption is a conjunction, each conjunct is tried separately,
in turn.
- These rules are used iteratively to descend through the structure of
the assumption as deeply as necessary.
If IMPS cannot recognize that the terms returned by a match are defined
in the appropriate sorts, then these assertions are returned as additional
minor premises that must later be grounded to complete the derivation.
backchain-backwards-inference
A sequent node assumption.
This primitive inference procedure
works the same way as backchain, except that subformulas of the
assumption of the forms s=t, 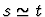 ,
,
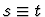 are used from
right to left.
are used from
right to left.
backchain-through-formula-inference
A sequent node assumption.
Similar to backchain, except
that it does not backchain through equivalences, i.e., formulas of
the form s=t, 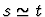 ,
or
,
or
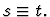
choice
None.
This primitive inference procedure
implements a version of the axiom of choice.
| Conclusion |
![$\Gamma \Rightarrow
\exists f\mbox{:}[\sigma_1,\ldots,\sigma_n,\tau],
\forall x_1\mbox{:}\sigma^{\prime}_{1},\ldots,
x_n\mbox{:}\sigma^{\prime}_{n}, \varphi$](img651.gif) |
| Premise |
![$\Gamma \Rightarrow
\forall x_1\mbox{:}\sigma^{\prime}_{1},\ldots,
x_n\mbox{:...
..._{n},
\exists y_f\mbox{:}\tau,
\varphi[{y_f}/{f(x_1,\ldots,x_n)}]_{\rm all}$](img652.gif) |
Notes:
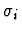 and
and
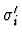 have the same type for all
i with
have the same type for all
i with
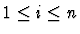 .
.
- The command fails if there is any occurrence of f in
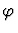 which is not in an application of the form
which is not in an application of the form
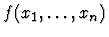 .
.
contraposition
A sequent node assumption 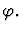
This primitive inference
procedure interchanges the given sequent's assertion and the
assumption 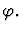
| Conclusion |
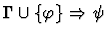 |
| Premise |
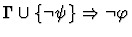 |
cut
A sequent node to be the major premise.
| Conclusion |
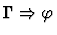 |
| Major Premise |
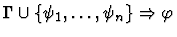 |
Minor Premises
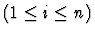 |
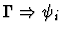 |
Notes:
- The major premise is the sequent
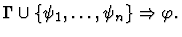
definedness
None.
This primitive inference
procedure applies to a sequent whose assertion is a definedness
statement of the form
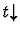 .
The primitive inference procedure
first tests whether the context entails the definedness of t. If
the test fails, the primitive inference then tries to reduce the
sequent to a set of simpler sequents.
.
The primitive inference procedure
first tests whether the context entails the definedness of t. If
the test fails, the primitive inference then tries to reduce the
sequent to a set of simpler sequents.
defined-constant-unfolding
- A list of paths
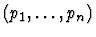 to occurrences of a defined
constant c.
to occurrences of a defined
constant c.
- The constant c itself.
This primitive inference procedure replaces
occurrences of the defined constant c at the paths pi by its
unfolding e.
direct-inference
None.
This primitive inference procedure
applies an analogue of an introduction rule of Gentzen's sequent
calculus (in reverse), based on the lead constructor of the assertion
of the given sequent.
| Conclusion |
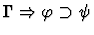 |
| Premise |
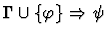 |
| Conclusion |
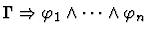 |
Premises
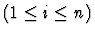 |
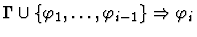 |
| Conclusion |
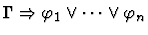 |
| Premise |
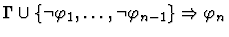 |
| Conclusion |
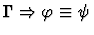 |
| Premises |
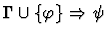 |
| |
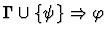 |
| Conclusion |
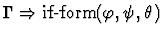 |
| Premises |
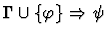 |
| |
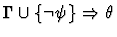 |
| Conclusion |
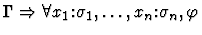 |
| Premise |
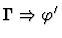 |
Notes:
-
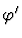 is obtained from
is obtained from 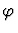 by renaming the
variables among
by renaming the
variables among
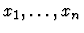 which are free in both
which are free in both 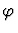 and
the context
and
the context 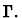
disjunction-elimination
A sequent node.
NO DESCRIPTION.
eliminate-iota
A path p to an iota-expression
occurrence in the assertion.
This primitive inference
procedure applies to a sequent whose assertion is an atomic formula or
negated atomic formula containing a specified occurrence of an
iota-expression. The command reduces the sequent to an equivalent
sequent in which the specified iota-expression occurrence is
``eliminated.''
| Conclusion |
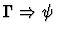 |
| Major Premise |
![$\Gamma \Rightarrow \exists y\mbox{:}\sigma,
(\varphi[{y}/{x}]_{\rm free} \wed...
...rall z\mbox{:}\sigma, (\varphi[{z}/{x}]_{\rm free}
\supset z=y) \wedge \psi')$](img676.gif) |
| Conclusion |
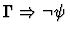 |
| Major Premise |
![$\Gamma \Rightarrow \exists y\mbox{:}\sigma,
(\varphi[{y}/{x}]_{\rm free} \wedge
\forall z\mbox{:}\sigma, (\varphi[{z}/{x}]_{\rm free}
\supset z=y)) \supset$](img678.gif) |
| |
![$\exists y\mbox{:}\sigma,
(\varphi[{y}/{x}]_{\rm free} \supset
\neg\psi')$](img679.gif) |
Notes:
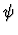 is an atomic formula.
is an atomic formula.
-
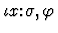 is the
expression located at the path p in
is the
expression located at the path p in 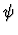 .
.
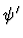 is the result of replacing the i-th
iota-expression occurrence in
is the result of replacing the i-th
iota-expression occurrence in 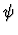 with y.
with y.
- The occurrence of
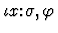 in
in
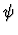 is within some argument component s of
is within some argument component s of 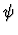 .
Moreover, the
occurrence is an extended application component of s, where a is
an extended application component of b if either a is bor b is an application of kind
.
Moreover, the
occurrence is an extended application component of s, where a is
an extended application component of b if either a is bor b is an application of kind 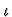 and a is an extended
application component of a component of b.
and a is an extended
application component of a component of b.
existential-generalization
A sequent node
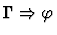 .
.
This primitive inference
procedure proves an existential assertion by exhibiting witnesses.
| Conclusion |
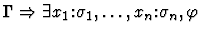 |
| Premise |
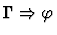 |
Notes:
- The command will fail unless the parameter sequent node is of
the form
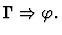
extensionality
None.
If the sequent node assertion is an
equality or quasi-equality or the negation of an equality or
quasi-equality of n-ary functions, this primitive inference applies
the extensionality principle.
| Conclusion |
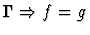 |
| Major Premise |
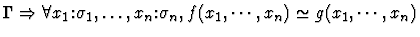 |
| Minor Premise |
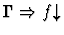 |
| Minor Premise |
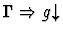 |
| Conclusion |
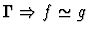 |
| Major Premise |
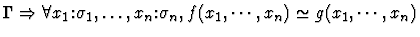 |
| Minor Premise |
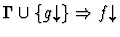 |
| Minor Premise |
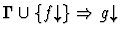 |
| Conclusion |
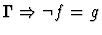 |
| Premise |
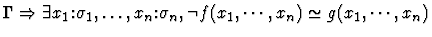 |
| Conclusion |
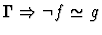 |
| Premise |
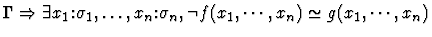 |
Notes:
- If the sorts of f and g are
![$[\alpha_1,\ldots,\alpha_n,\alpha_{n+1}]$](img95.gif) and
and
![$[\beta_1,\ldots,\beta_n,\beta_{n+1}]$](img690.gif) ,
respectively, then
,
respectively, then
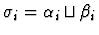 for all i with
for all i with
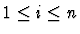 .
.
- A sequent node corresponding to a minor premise is not
created if the truth of the minor premise is immediately apparent to
IMPS.
- If f and g are of kind
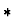 ,
then ``='' is used in
place of ``
,
then ``='' is used in
place of ``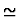 '' in the premise.
'' in the premise.
force-substitution
- Paths. A list of paths
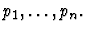
- Replacements. A list of expressions
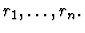
This primitive inference procedure changes part
of the sequent assertion. It yields two or more new subgoals. One
subgoal is obtained from the original sequent assertion by replacing
the subexpression ei at the path pi with ri. The other subgoals
assert that the replacements are sound.
| Conclusion |
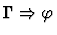 |
| Major Premise |
![$\Gamma \Rightarrow \varphi[r_i/e_i]$](img740.gif) |
Minor Premises
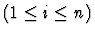 |
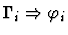 |
Notes:
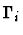 is the local context of
is the local context of
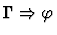 at
the path pi.
at
the path pi.
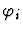 is:
is:
-
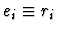 if ei is a formula and the parity of the path pi is
0.
if ei is a formula and the parity of the path pi is
0.
-
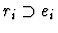 if ei is a formula and the parity of the path
pi is 1.
if ei is a formula and the parity of the path
pi is 1.
-
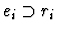 if ei is a formula and the parity of the path pi is -1.
if ei is a formula and the parity of the path pi is -1.
-
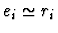 in all other cases.
in all other cases.
incorporate-antecedent
A sequent node assumption 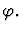
This primitive inference
procedure does the reverse of direct-inference on an
implication.
| Conclusion |
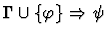 |
| Premise |
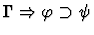 |
insistent-direct-inference
None.
This primitive inference
procedure is equivalent to disabling all quasi-constructors and
then calling direct-inference.
insistent-simplification
None.
This primitive inference
procedure is equivalent to disabling all quasi-constructors and
then calling simplification.
macete-application-at-paths
- A list of paths
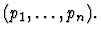
- A macete.
This primitive inference
procedure applies the argument macete to the sequent node assertion at
those occurrences specified by the paths
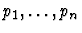 .
.
macete-application-with-minor-premises-at-paths
- A list of paths
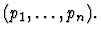
- A macete
This primitive inference
procedure applies the argument macete to the given sequent node, in
the same way as macete-application, but with the following important
difference: whenever the truth or falsehood of a convergence
requirement cannot be determined by the simplifier, the assertion is
posted as a additional subgoal to be proved.
raise-conditional-inference
A list of paths
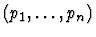 to
conditional subexpressions.
to
conditional subexpressions.
This primitive inference procedure will ``raise'' a subset
of the conditional expressions (i.e., expressions whose lead
constructor is if), specified by the paths pi, in the
assertion of the given sequent
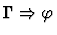 .
.
For the moment, let us assume that n=1. Suppose
the conditional expression in 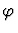 located at p1 is the a-th
occurrence of
located at p1 is the a-th
occurrence of
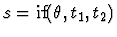 in
in 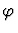 ;
the smallest
formula containing the a-th occurrence of s in
;
the smallest
formula containing the a-th occurrence of s in 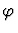 is the
b-th occurrence of
is the
b-th occurrence of 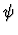 in
in 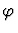 ;
and the a-th occurrence of
s in
;
and the a-th occurrence of
s in 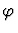 is the c-th occurrence of s in
is the c-th occurrence of s in 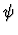 .
If every
free occurrence of a variable in s is also a free occurrence in
.
If every
free occurrence of a variable in s is also a free occurrence in
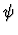 ,
the primitive inference procedure reduces the sequent to
,
the primitive inference procedure reduces the sequent to
and otherwise the primitive inference procedure fails.
Now assume n > 1. The primitive inference procedure will then simultaneously raise each
specified occurrence of a conditional expression in 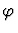 ,
in the
manner of the previous paragraph, if there are no conflicts between
the occurrences. The kinds of conflicts that can arise and how they
are resolved are listed below:
,
in the
manner of the previous paragraph, if there are no conflicts between
the occurrences. The kinds of conflicts that can arise and how they
are resolved are listed below:
- If two or more specified occurrences of a conditional expression
s in
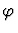 are contained in same smallest formula, they are
raised together.
are contained in same smallest formula, they are
raised together.
- If two or more specified occurrences of distinct conditional
expressions in
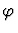 are contained in same smallest formula, at
most one of the occurrences is raised.
are contained in same smallest formula, at
most one of the occurrences is raised.
- If
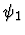 and
and 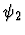 are the smallest formulas
respectively containing two specified occurrences of a conditional
expression in
are the smallest formulas
respectively containing two specified occurrences of a conditional
expression in 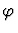 and
and 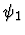 is a proper subexpression of
is a proper subexpression of
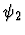 ,
then the first specified conditional expression is not
raised.
,
then the first specified conditional expression is not
raised.
simplification
None.
This primitive inference procedure simplifies the
assertion of the given sequent with respect to the context of the
sequent. It uses both theory-specific and general logical methods to
reduce the sequent to a logically equivalent sequent. The
theory-specific methods include algebraic simplification, deciding
rational linear inequalities, and applying rewrite rules.
simplification-with-minor-premises
None.
This primitive inference procedure is
the same as simplification except that, instead of failing
when convergence requirements are not verified, it posts the
unverified convergence requirements as additional subgoals to be
proved.
sort-definedness
None.
This primitive inference
procedure applies to a sequent whose assertion is a definedness
statement of the form
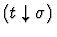 .
The primitive inference
procedure first tests whether the context entails the definedness of
t in
.
The primitive inference
procedure first tests whether the context entails the definedness of
t in 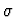 .
If the test fails, the primitive inference procedure
then tries to reduce the sequent to a set of simpler sequents. In
particular, when t is a conditional term if
.
If the test fails, the primitive inference procedure
then tries to reduce the sequent to a set of simpler sequents. In
particular, when t is a conditional term if
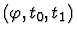 ,
it distributes the sort definedness assertion into the
consequent and alternative. If t0 and t1 are not themselves
conditional terms, the new subgoal has the assertion
if-form
,
it distributes the sort definedness assertion into the
consequent and alternative. If t0 and t1 are not themselves
conditional terms, the new subgoal has the assertion
if-form
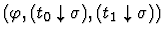 .
If one or both of them is a conditional term, then the sort
definedness assertion is recursively distributed into the consequents
and alternatives.
.
If one or both of them is a conditional term, then the sort
definedness assertion is recursively distributed into the consequents
and alternatives.
theorem-assumption
A formula which must be a theorem of
the context theory.
This primitive inference procedure adds the argument
theorem to the context of the given sequent.
universal-instantiation
A sequent node
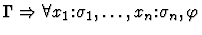 .
.
This primitive inference
procedure proves a formula by proving a universal.
| Conclusion |
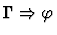 |
| Premise |
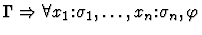 |
Notes:
- The command will fail unless the parameter sequent node is of
the form
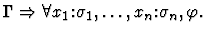
unordered-conjunction-direct-inference
None.
If the sequent node assertion is a
conjunction, this primitive inference procedure does a direct inference
without strengthening the context.
weakening
A set of formulas 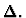
This primitive inference procedure
removes one or more assumptions you specify from the context
of the given sequent.
| Conclusion |
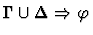 |
| Premise |
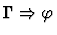 |



Next: 20. The Initial Theory
Up: 3. Reference Manual
Previous: 18. The Proof Commands
System Administrator
2000-07-23
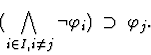
![]() located at p1 is the a-th
occurrence of
located at p1 is the a-th
occurrence of
![]() in
in ![]() ;
the smallest
formula containing the a-th occurrence of s in
;
the smallest
formula containing the a-th occurrence of s in ![]() is the
b-th occurrence of
is the
b-th occurrence of ![]() in
in ![]() ;
and the a-th occurrence of
s in
;
and the a-th occurrence of
s in ![]() is the c-th occurrence of s in
is the c-th occurrence of s in ![]() .
If every
free occurrence of a variable in s is also a free occurrence in
.
If every
free occurrence of a variable in s is also a free occurrence in
![]() ,
the primitive inference procedure reduces the sequent to
,
the primitive inference procedure reduces the sequent to ![]() ,
in the
manner of the previous paragraph, if there are no conflicts between
the occurrences. The kinds of conflicts that can arise and how they
are resolved are listed below:
,
in the
manner of the previous paragraph, if there are no conflicts between
the occurrences. The kinds of conflicts that can arise and how they
are resolved are listed below: